Question

如图，△ABC和△A′B′C是两个完全重合的直角三角板，∠B=30°，斜边长为16cm，三角板A′B′C绕直角顶点C顺时针旋转，当点A′落在AB边上时，点A′所转过的路径长为________cm．

Answer 1

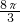
分析：根据三角形内角和和含30度的直角三角形三边的关系得到∠A=60°，AC=AB=8，在根据旋转的性质得CA′=CA，于是可判断△CAA′为等边三角形，所以∠ACA′=60°，然后根据弧长公式计算弧AA′的长度即可．
解答：∵∠ACB=90°，∠B=30°，AB=16，
∴∠A=60°，AC=AB=8，
∵三角板A′B′C绕直角顶点C顺时针旋转，点A′落在AB边上，
∴CA′=CA，
∴△CAA′为等边三角形，
∴∠ACA′=60°，
∴弧AA′的长度==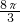（cm），
即点A′所转过的路径长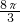cm．
故答案为．
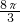点评：本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了弧长公式．