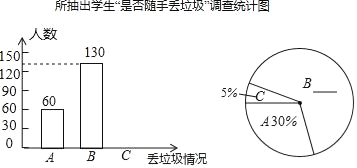
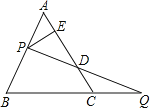
题目内容
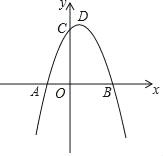
【题目】如图,已知抛物线y=ax2+2x+8与x轴交于A,B两点,与y轴交于点C,且B(4,0).
(1)求抛物线的解析式及其顶点D的坐标;
(2)如果点P(p,0)是x轴上的一个动点,则当|PC﹣PD|取得最大值时,求p的值;
(3)能否在抛物线第一象限的图象上找到一点Q,使△QBC的面积最大,若能,请求出点Q的坐标;若不能,请说明理由.
【答案】(1) y=﹣(x﹣1)2+9 ,D(1,9); (2)p=﹣8;(3)存在点Q(2,8)使△QBC的面积最大.
【解析】
(1)把点B的坐标代入y=ax2+2x+8求得a的值,即可得到该抛物线的解析式,再把所得解析式配方化为顶点式,即可得到抛物线顶点D的坐标;
(2)由题意可知点P在直线CD上时,|PC﹣PD|取得最大值,因此,求得点C的坐标,再求出直CD的解析式,即可求得符合条件的点P的坐标,从而得到p的值;
(3)由(1)中所得抛物线的解析式设点Q的坐标为(m,﹣m2+2m+8)(0<m<4),然后用含m的代数式表达出△BCQ的面积,并将所得表达式配方化为顶点式即可求得对应点Q的坐标.
(1)∵抛物线y=ax2+2x+8经过点B(4,0),
∴16a+8+8=0,
∴a=﹣1,
∴抛物线的解析式为y=﹣x2+2x+8=﹣(x﹣1)2+9,
∴D(1,9);
(2)∵当x=0时,y=8,
∴C(0,8).
设直线CD的解析式为y=kx+b.
将点C、D的坐标代入得:![]() ,解得:k=1,b=8,
,解得:k=1,b=8,
∴直线CD的解析式为y=x+8.
当y=0时,x+8=0,解得:x=﹣8,
∴直线CD与x轴的交点坐标为(﹣8,0).
∵当P在直线CD上时,|PC﹣PD|取得最大值,
∴p=﹣8;
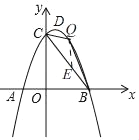
(3)存在,
理由:如图,由(2)知,C(0,8),
∵B(4,0),
∴直线BC的解析式为y=﹣2x+8,
过点Q作QE∥y轴交BC于E,
设Q(m,﹣m2+2m+8)(0<m<4),则点E的坐标为:(m,﹣2m+8),
∴EQ=﹣m2+2m+8﹣(﹣2m+8)=﹣m2+4m,
∴S△QBC=![]() (﹣m2+4m)×4=﹣2(m﹣2)2+8,
(﹣m2+4m)×4=﹣2(m﹣2)2+8,
∴m=2时,S△QBC最大,此时点Q的坐标为:(2,8).

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案