题目内容
如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6,求PA+PB的最小值.

解:∵MN=20,
∴⊙O的半径=10,
连接OA、OB,
在Rt△OBD中,OB=10,BD=6,
∴OD=![]() =8,
=8,
同理,在Rt△AOC中,OA=10,AC=8,
∴OC=![]() =6,
=6,
∴CD=8+6=14,
作点B关于MN的对称点B′,连接AB′,则AB′即为PA+PB的最小值,B′D=BD=6,过点B′作AC的垂线,交AC的延长线于点E,
在Rt△AB′E中,
∵AE=AC+CE=8+6=14,B′E=CD=14,
∴AB′=14![]() ,
,
∴PA+PB的最小值是14![]() .
.


练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
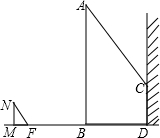 如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?
如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?
 ,求A点横坐标的数值.
,求A点横坐标的数值.
 ,求A点横坐标的数值.
,求A点横坐标的数值.
 ,求A点横坐标的数值.
,求A点横坐标的数值.