题目内容
 在锐角△ABC中,∠BAC=60°,BD、CE为高,F是BC的中点,连接DE、EF、FD.则以下结论中一定正确的个数有( )
在锐角△ABC中,∠BAC=60°,BD、CE为高,F是BC的中点,连接DE、EF、FD.则以下结论中一定正确的个数有( )①EF=FD;
②AD:AB=AE:AC;
③△DEF是等边三角形;
④BE+CD=BC;
⑤当∠ABC=45°时,BE=
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
分析:①EF、FD是直角三角形斜边上的中线,都等于BC的一半;②可证△ABD∽△ACE;③证明∠EFD=60°;④假设结论成立,在BC上取满足条件的点H,证明其存在性;⑤当∠ABC=45°时,EF不一定是BC边的高.
解答:解:①∵BD、CE为高,∴△BEC、△BDC是直角三角形.
∵F是BC的中点,∴EF=DF=
BC.故正确;
②∵∠ADB=∠AEC=90°,∠A公共,∴△ABD∽△ACE,得AD:AB=AE:AC.故正确;
③∵∠A=60°,∴∠ABC+∠ACB=120°.
∵F是BC的中点,∴EF=BF,DF=CF.∴∠ABF=∠BEF,∠ACB=∠CDF.
∴∠BFE+∠CFD=120°,∠EFD=60°.又EF=FD,∴△DEF是等边三角形.故正确;
④若BE+CD=BC,则可在BC上截取BH=BE,则HC=CD.
∵∠A=60°,∴∠ABC+∠ACB=120°.又∵BH=BE,HC=CD,
∴∠BHE+∠CHD=120°,∠EHD=60°.
所以存在满足条件的点,假设成立,但一般情况不一定成立,故错误;
⑤当∠ABC=45°时,在Rt△BCE中,BC=
BE,在Rt△ABD中,AB=2AD,
由B、C、D、E四点共圆可知,△ADE∽△ABC,
∴
=
=
,即
=
,∴BE=
DE,故正确;
故此题选C.
∵F是BC的中点,∴EF=DF=
| 1 |
| 2 |
②∵∠ADB=∠AEC=90°,∠A公共,∴△ABD∽△ACE,得AD:AB=AE:AC.故正确;
③∵∠A=60°,∴∠ABC+∠ACB=120°.
∵F是BC的中点,∴EF=BF,DF=CF.∴∠ABF=∠BEF,∠ACB=∠CDF.
∴∠BFE+∠CFD=120°,∠EFD=60°.又EF=FD,∴△DEF是等边三角形.故正确;
④若BE+CD=BC,则可在BC上截取BH=BE,则HC=CD.
∵∠A=60°,∴∠ABC+∠ACB=120°.又∵BH=BE,HC=CD,
∴∠BHE+∠CHD=120°,∠EHD=60°.

所以存在满足条件的点,假设成立,但一般情况不一定成立,故错误;
⑤当∠ABC=45°时,在Rt△BCE中,BC=
| 2 |
由B、C、D、E四点共圆可知,△ADE∽△ABC,
∴
| DE |
| BC |
| AD |
| AB |
| 1 |
| 2 |
| DE | ||
|
| 1 |
| 2 |
| 2 |
故此题选C.
点评:此题考查了相似三角形的判定和性质,综合性很强.

练习册系列答案
相关题目
在锐角△ABC中,a、b、c分别表示为∠A、∠B、∠C的对边,O为其外心,则O点到三边的距离之比为( )
| A、a:b:c | ||||||
B、
| ||||||
| C、cosA:cosB:cosC | ||||||
| D、sinA:sinB:sinC |
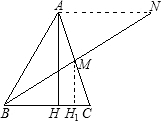 在锐角△ABC中,最大的高线AH等于中线BM,求证:∠B<60°(如图).
在锐角△ABC中,最大的高线AH等于中线BM,求证:∠B<60°(如图). 如图,在锐角△ABC中,∠BAC=60°,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①B、E、D、C四点共圆;②AD•AC=AE•AB;③△DEF是等边三角形;④当∠ABC=45°时,BE=
如图,在锐角△ABC中,∠BAC=60°,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①B、E、D、C四点共圆;②AD•AC=AE•AB;③△DEF是等边三角形;④当∠ABC=45°时,BE=