��Ŀ����
��ͼ��ʾ���ı���OABC�Ǿ��Σ���A��C������ֱ�Ϊ��-3��0������0��1������D���߶�BC �ϵĶ��㣨��˵�B��C���غϣ�������D��ֱ��y=| 1 |
| 2 |
��1���ǡ�ODE�����ΪS����S��b�ĺ�����ϵʽ��
��2������E���߶�0A��ʱ����tan��DEO=
| 1 |
| 2 |


��������1��Ҫ��ʾ����ODE�������Ҫ������������ۣ��������E��OA���ϣ�ֻ�������������εĵױ�OE����E������꣩�ߣ�D�������꣩�����������������ʽ���ɣ��������E��AB���ϣ���ʱ��ODE��������ó�����OABC�������ȥ��OCD����OAE����BDE�������
��2���ص�������һ��ƽ���ı��Σ��������ƽ���ı������±��ϵĸ߲��䣬��˾����ص���������Ƿ�仯�����ؾ��ǿ����ƽ���ı�������OA���ϵ��߶γ����Ƿ�仯��
��2���ص�������һ��ƽ���ı��Σ��������ƽ���ı������±��ϵĸ߲��䣬��˾����ص���������Ƿ�仯�����ؾ��ǿ����ƽ���ı�������OA���ϵ��߶γ����Ƿ�仯��
���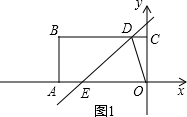 �⣺��1�����ı���OABC�Ǿ��Σ���A��C������ֱ�Ϊ��-3��0������0��1����
�⣺��1�����ı���OABC�Ǿ��Σ���A��C������ֱ�Ϊ��-3��0������0��1����
��B��-3��1����
��ֱ�߾�����A��-3��0��ʱ����b=
��
��ֱ�߾�����B��-3��1��ʱ����b=
��
��ֱ�߾�����C��0��1��ʱ����b=1��
����ֱ��������OAB�Ľ�����OA��ʱ����1��b��
����ͼ1��
��ʱE��-2b��0����
��S=
OE•CO=
��2b��1=b��
����ֱ��������OAB�Ľ�����BA��ʱ����
��b��
����ͼ2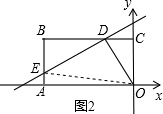
��ʱE��-3��b-
����D��2-2b��1����
��S=S��-��S��OCD+S��OAE+S��DBE��
=3-[
��2b-2����1+
����5-2b��•��
-b��+
��3��b-
��]
=
b-b2��
��S=
��
��2����ͼ3����O1A1��CB�ཻ�ڵ�M��OA��C1B1�ཻ�ڵ�N�������O1A1B1C1�����OABC���ص����ֵ������Ϊ
�ı���DNEM�������
������֪��DM��NE��DN��ME��
���ı���DNEMΪƽ���ı��Σ�
������Գ�֪����MED=��NED��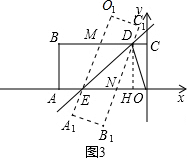
�֡�MDE=��NED��
���MED=��MDE��
��MD=ME��
��ƽ���ı���DNEMΪ���Σ�
����D��DH��OA������ΪH��
������֪��tan��DEO=
��
��
=
��DH=1��
��HE=2��
������DNEM�ı߳�Ϊa��
����Rt��DHN�У��ɹ��ɶ���֪��a2=��2-a��2+12��
��a=
��
��S�ı���DNEM=NE•DH=
��
�����O1A1B1C1�����OABC���ص����ֵ�����������仯�����ʼ��Ϊ
��
 �⣺��1�����ı���OABC�Ǿ��Σ���A��C������ֱ�Ϊ��-3��0������0��1����
�⣺��1�����ı���OABC�Ǿ��Σ���A��C������ֱ�Ϊ��-3��0������0��1������B��-3��1����
��ֱ�߾�����A��-3��0��ʱ����b=
| 3 |
| 2 |
��ֱ�߾�����B��-3��1��ʱ����b=
| 5 |
| 2 |
��ֱ�߾�����C��0��1��ʱ����b=1��
����ֱ��������OAB�Ľ�����OA��ʱ����1��b��
| 3 |
| 2 |
��ʱE��-2b��0����
��S=
| 1 |
| 2 |
| 1 |
| 2 |
����ֱ��������OAB�Ľ�����BA��ʱ����
| 3 |
| 2 |
| 5 |
| 2 |

��ʱE��-3��b-
| 3 |
| 2 |
��S=S��-��S��OCD+S��OAE+S��DBE��
=3-[
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=
| 5 |
| 2 |
��S=
|
��2����ͼ3����O1A1��CB�ཻ�ڵ�M��OA��C1B1�ཻ�ڵ�N�������O1A1B1C1�����OABC���ص����ֵ������Ϊ
�ı���DNEM�������
������֪��DM��NE��DN��ME��
���ı���DNEMΪƽ���ı��Σ�
������Գ�֪����MED=��NED��

�֡�MDE=��NED��
���MED=��MDE��
��MD=ME��
��ƽ���ı���DNEMΪ���Σ�
����D��DH��OA������ΪH��
������֪��tan��DEO=
| 1 |
| 2 |
��
| DH |
| HE |
| 1 |
| 2 |
��HE=2��
������DNEM�ı߳�Ϊa��
����Rt��DHN�У��ɹ��ɶ���֪��a2=��2-a��2+12��
��a=
| 5 |
| 4 |
��S�ı���DNEM=NE•DH=
| 5 |
| 4 |
�����O1A1B1C1�����OABC���ص����ֵ�����������仯�����ʼ��Ϊ
| 5 |
| 4 |
������������һ����̬ͼ���е�����Ƿ�仯�����⣬��һ��ͼ�ε�����Ƿ�仯���ؼ��ǿ������������ļ������Ƿ�仯������������ӱ���Ǹ����ɶ�õĺ��⣬����������ѧ����˼ά���������ѶȽϴ������Ե����ֶȣ�

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ��ʾ���ı���OABCΪ�����Σ��߳�Ϊ6����A��C�ֱ���x�ᣬy����������ϣ���D��OA�ϣ���D������Ϊ��2��0����P��OB�ϵ�һ���㣬����PD+PA�͵���Сֵ�ǣ�������
��ͼ��ʾ���ı���OABCΪ�����Σ��߳�Ϊ6����A��C�ֱ���x�ᣬy����������ϣ���D��OA�ϣ���D������Ϊ��2��0����P��OB�ϵ�һ���㣬����PD+PA�͵���Сֵ�ǣ������� �˵�B��C���غϣ�������D��ֱ��y=-
�˵�B��C���غϣ�������D��ֱ��y=- ��2013•������һģ����ͼ��ʾ���ı���OABC�Ǿ��Σ���A��C������ֱ�Ϊ��6��0������0��2������D���߶�BC�ϵĶ��㣨��˵�B��C���غϣ�������D��ֱ��y=-
��2013•������һģ����ͼ��ʾ���ı���OABC�Ǿ��Σ���A��C������ֱ�Ϊ��6��0������0��2������D���߶�BC�ϵĶ��㣨��˵�B��C���غϣ�������D��ֱ��y=-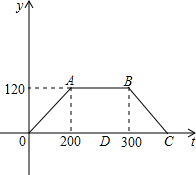 С���μ�������ʻ��ѵ����ʵ�ʲ�������ʱ����Ҫ������������١��������С��ƶ���������������̣��ڼ��ٺͼ����˶������У�·�̺��ٶȾ������ϵs=
С���μ�������ʻ��ѵ����ʵ�ʲ�������ʱ����Ҫ������������١��������С��ƶ���������������̣��ڼ��ٺͼ����˶������У�·�̺��ٶȾ������ϵs= ��ͼ��ʾ���ı���ABCD��A��B��C��D����0Ϊλ�����ģ�λ�Ʊ�Ϊ1��2�����A�Ķ�Ӧ���ǵ�
��ͼ��ʾ���ı���ABCD��A��B��C��D����0Ϊλ�����ģ�λ�Ʊ�Ϊ1��2�����A�Ķ�Ӧ���ǵ�