题目内容
如图,⊙O中半径OA=2,∠AOB=60°,P为
上的点,PM⊥OA于M,
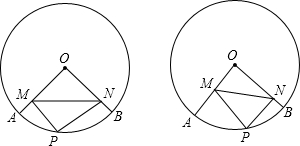
PN⊥OB于N.
(1)若P是
的中点,求MN的长;
(2)若点P不是
的中点,则MN的长度是否发生变化?请说明理由;
(3)若∠AOB=45°,求MN的长.(不用证明)
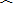 |
| AB |

PN⊥OB于N.
(1)若P是
 |
| AB |
(2)若点P不是
 |
| AB |
(3)若∠AOB=45°,求MN的长.(不用证明)

(1)连接OP,
∵P为
 |
| AB |
∴∠AOP=∠BOP=
| 1 |
| 2 |
∵PM⊥OA于Mcos∠AOP=
| OM |
| OP |
| ||
| 2 |
∴OM=
| 3 |
同理ON=
| 3 |
∴OM=ON,
∵∠AOB=60°,
∴△OMN为等边三角形
∴MN=
| 3 |
(2)长度不变.
设Pn为
 |
| AB |
En,Fn由于∠EPF=∠EnPnFn=120°
∴EF=EnFn
又MN,MnNn分别为△PEF,△PnEnFn的中位线
∴MN=
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=MnNn
(3)由(1),(2)可知P点取
 |
| AB |
故当∠AOB=45°时,
让点P与点A重合,
PN=
| ||
| 2 |
| 2 |
MN=
| 2 |

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目

 PN⊥OB于N.
PN⊥OB于N.
 上的点,PM⊥OA于M,
上的点,PM⊥OA于M,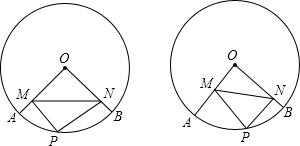 PN⊥OB于N.
PN⊥OB于N. 上的点,PM⊥OA于M,PN⊥OB于N.
上的点,PM⊥OA于M,PN⊥OB于N. 的中点,求MN的长;
的中点,求MN的长; 的中点,则MN的长度是否发生变化?请说明理由;
的中点,则MN的长度是否发生变化?请说明理由;