题目内容
在△ABC中，
，
，直线
经过点
，且
于
，
于E.
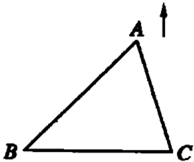
（1）当直线绕点旋转到图1的位置时，求证： ①
≌
；②
.
（2）当直线绕点旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由.
【答案】
详见解析
【解析】
试题分析：（1）①要证
，已知一直角
和一边
对应相等，由题意根据同角的余角相等，可得另一内角
，再由
即可判定.
②由①容易得出：
,
.而
,故
.解答此类问题的关键就是找出与结论中相等的线段，利用等量代换即可求解.
（2）同理，根据上一小题的解题思路，易得结论①成立,而结论②不成立.
试题解析：(1)①∵
∴
∵
∴
∴
∵,
∴
在
和
中
∴
②∵
∴
∵
∴
(1)中的结论①成立，结论②不成立。理由如下：
∵
∴
∵
∴
∴
∵,
∴
在和中
∴
∴
∵
∴
考点：1、三角形全等的判定；2、三角形全等的性质.
练习册系列答案
相关题目
20、如图，在△ABC中，BC边不动，点A是一个动点．当点A竖直向上运动，∠A越来越小，∠B、∠C越来越大．若∠A减少α度，∠B增加β度，∠C增加γ度，请写出α、β、γ三者之间的等量关系，并说明你是如何得到的．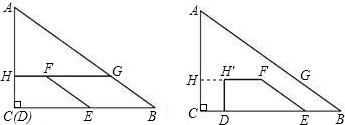
30、如图，在△ABC中，AB=AC，D是BC的中点，连接AD．DE⊥AB，DF⊥AC，E，F是垂足．图中共有多少对全等三角形？请直接用“≌”符号把它们分别表示出来．（不要求证明）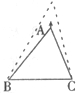
14、如图，在△ABC中，BC边不动，点A竖直向上运动，∠A越来越小，∠B，∠C越来越大．若∠A减小x°，∠B增加y°，∠C增加z°，则x，y，z之间的关系是（ ）
学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，也可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=