题目内容
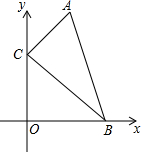 如图,在直角坐标系中,点A、B的坐标分别为(2,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上.
如图,在直角坐标系中,点A、B的坐标分别为(2,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上.(1)求过点A、B两点的直线解析式;
(2)在运动的过程中,当△ABC周长最小时,求点C的坐标;
(3)在运动的过程中,当△ABC是以AB为底的等腰三角形时,求点C的坐标.
考点:一次函数综合题
专题:
分析:(1)根据待定系数法,可得函数解析式;
(2)根据线段垂直平分线的性质,可得B′点,根据线段的性质,可得AB′,根据待定系数法求函数解析式,根据自变量的值,可得相应的函数值;
(3)根据等腰三角形的判定,可得AC=BC,根据解方程,可得C点的坐标.
(2)根据线段垂直平分线的性质,可得B′点,根据线段的性质,可得AB′,根据待定系数法求函数解析式,根据自变量的值,可得相应的函数值;
(3)根据等腰三角形的判定,可得AC=BC,根据解方程,可得C点的坐标.
解答:解:(1)设AB的解析式为y=kx+b,图象经过点(2,4)和(3,0),得
,解得
,
AB两点的直线解析式y=-4x+12;
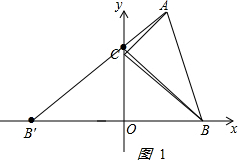
(2)如图1:
 ,
,
作B点关于y轴的对称点B′,连接AB′,交y轴于C点,
B′点的坐标是(-3,0),
设AB′的函数解析式为y=kx+b,图象经过(-3,0),(2,4),得
,
解得
.
AB′的函数解析式为y=
x+
,
自变量的值为零时,y=
当△ABC周长最小时,C点坐标为(0,
);
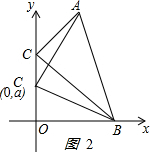
(3)图2:
 ,
,
设C点坐标为(0,a),当△ABC是以AB为底的等腰三角形时,BC=AC,平方,得
BC2=AC2,22+(4-a)2=32+a2,
化简,得8a=11,
解得a=
,
故点C的坐标为(0,
).
|
|
AB两点的直线解析式y=-4x+12;
(2)如图1:
 ,
,作B点关于y轴的对称点B′,连接AB′,交y轴于C点,
B′点的坐标是(-3,0),
设AB′的函数解析式为y=kx+b,图象经过(-3,0),(2,4),得
|
解得
|
AB′的函数解析式为y=
| 4 |
| 5 |
| 12 |
| 5 |
自变量的值为零时,y=
| 12 |
| 5 |
当△ABC周长最小时,C点坐标为(0,
| 12 |
| 5 |
(3)图2:
 ,
,设C点坐标为(0,a),当△ABC是以AB为底的等腰三角形时,BC=AC,平方,得
BC2=AC2,22+(4-a)2=32+a2,
化简,得8a=11,
解得a=
| 11 |
| 8 |
故点C的坐标为(0,
| 11 |
| 8 |
点评:本题考查了一次函数综合题,(1)利用了待定系数法求函数解析式;(2)利用了线段垂直平分线的性质,两点之间线段最短;(3)利用了等腰三角形的判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
钟表8点30分时,时针和分针所成的夹角是( )
| A、85° | B、75° |
| C、70° | D、60° |
下面计算错误的是( )
| A、(-11)+(-17)=-28 | ||||||
B、
| ||||||
C、(-
| ||||||
| D、(-9)+9=0 |
若不等式组
有解,则a的取值范围是( )
|
| A、a>2 | B、a<2 |
| C、a≤2 | D、a≥2 |
若样本x1,x2,x3,…xn的平均数是10,方差是2,则对于样本(x1+1),(x2+1),(x3+1),…,(xn+1),下列结论中正确的是( )
| A、平均数为10,方差是2 |
| B、平均数是11,方差为3 |
| C、平均数为11,方差为2 |
| D、平均数为12,方差为4 |
 用反正法证明命题“如图,如果AB∥CD,AB∥EF,那么CD∥EF”时,证明的第一个步骤是( )
用反正法证明命题“如图,如果AB∥CD,AB∥EF,那么CD∥EF”时,证明的第一个步骤是( )| A、假设AB不平行于CD |
| B、假设AB不平行于EF |
| C、假设CD∥EF |
| D、假设CD不平行于EF |
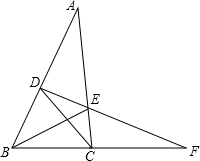 如图,在△ABC,点D、E分别在AB、AC上,连结DE并延长交BC的延长线于点F,连结DC、BE,若∠BDE+∠BCE=180°.请写出图中的两对相似三角形(不另外添加字母和线),并选择其中的一对进行证明.
如图,在△ABC,点D、E分别在AB、AC上,连结DE并延长交BC的延长线于点F,连结DC、BE,若∠BDE+∠BCE=180°.请写出图中的两对相似三角形(不另外添加字母和线),并选择其中的一对进行证明.