题目内容
若△ABC≌△A′B′C′,且∠A:∠B:∠C=2:3:4,则∠A′:∠B′为
- A.2:4
- B.2:3
- C.3:4
- D.3:2
B
分析:根据△ABC≌△A′B′C′,可知∠A=∠A′,∠B=∠B′,∠C=∠C′,已知∠A:∠B:∠C=2:3:4,即可得∠A′:∠B′的值.
解答:∵△ABC≌△A′B′C′,
∴∠A=∠A′,∠B=∠B′,∠C=∠C′,
已知∠A:∠B:∠C=2:3:4,
∴∠A′:∠B′=2:3.
故选B.
点评:本题考查了全等三角形的性质,解题的关键在于熟练掌握两全等三角形的对应边、对应角间的对应关系.
分析:根据△ABC≌△A′B′C′,可知∠A=∠A′,∠B=∠B′,∠C=∠C′,已知∠A:∠B:∠C=2:3:4,即可得∠A′:∠B′的值.
解答:∵△ABC≌△A′B′C′,
∴∠A=∠A′,∠B=∠B′,∠C=∠C′,
已知∠A:∠B:∠C=2:3:4,
∴∠A′:∠B′=2:3.
故选B.
点评:本题考查了全等三角形的性质,解题的关键在于熟练掌握两全等三角形的对应边、对应角间的对应关系.

练习册系列答案
相关题目
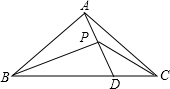 如图,在等腰直角三角形ABC中,∠BAC=90°,在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连结PC,若△ABC的面积为4cm2,则△BPC的面积为( )
如图,在等腰直角三角形ABC中,∠BAC=90°,在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连结PC,若△ABC的面积为4cm2,则△BPC的面积为( )| A、4cm2 | B、3cm2 | C、2cm2 | D、8cm2 |
 7、如图,D是线段AB,BC的垂直平分线的交点,若∠ABC=50°,则∠ADC的大小是( )
7、如图,D是线段AB,BC的垂直平分线的交点,若∠ABC=50°,则∠ADC的大小是( )