题目内容
 24、如图,BC⊥CD,∠1=∠2=∠3,∠4=60°,∠5=∠6.
24、如图,BC⊥CD,∠1=∠2=∠3,∠4=60°,∠5=∠6.(1)CO是△BCD的高吗?为什么?
(2)∠5的度数是多少?
(3)求四边形ABCD各内角的度数.
分析:(1)要想验证CO是△BCD的高就得证明CO与DB相交所成的角中有没有90°的角;
(2)利用三角形的内角和定理求∠5的度数;
(3)求∠ABC的度数时,注意利用两个三角形的内角和加在一起是360°.
(2)利用三角形的内角和定理求∠5的度数;
(3)求∠ABC的度数时,注意利用两个三角形的内角和加在一起是360°.
解答:解:(1)CO是△BCD的高.
理由:在△BDC中,∵∠BCD=90°
∴∠1+∠2=90°
又∵∠1=∠3,
∴∠1+∠3=90°
∴CO⊥DB,
∴CO是△BCD的高.
(2)∠5=90°-∠4=90°-60°=30度.
(3)∠CDA=∠1+∠4=45°+60°=105°,
∠DCB=90°,
∠DAB=∠5+∠6=30°+30°=60°,
∠ABC=105°.
理由:在△BDC中,∵∠BCD=90°
∴∠1+∠2=90°
又∵∠1=∠3,
∴∠1+∠3=90°
∴CO⊥DB,
∴CO是△BCD的高.
(2)∠5=90°-∠4=90°-60°=30度.
(3)∠CDA=∠1+∠4=45°+60°=105°,
∠DCB=90°,
∠DAB=∠5+∠6=30°+30°=60°,
∠ABC=105°.
点评:本题考查的知识点为:垂直定义,及三角形的内角和等于180°.

练习册系列答案
相关题目
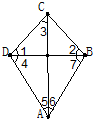 27、如图,BC⊥CD,∠1=∠2=∠3,∠4=60°,∠5=∠6.
27、如图,BC⊥CD,∠1=∠2=∠3,∠4=60°,∠5=∠6. 如图,
如图,
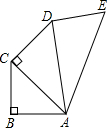 如图AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则AE等于
如图AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则AE等于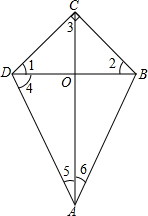 如图,BC⊥CD,∠1=∠2=∠3,∠4=70°,∠5=∠6
如图,BC⊥CD,∠1=∠2=∠3,∠4=70°,∠5=∠6