题目内容
如图，已知平行四边形ABCD的面积为24cm2，E为AB的中点，连接DE，则△ODE的面积为
- A.3cm2
- B.4cm2
- C.6cm2
- D.12cm2
A
分析：由图形及平行四边形的性质可得S△ABC=
S平行四边形ABCD，S△BED=S△ABD，S△OED=S△BED，从而结合平行四边形ABCD的面积为24cm2，可得出△ODE的面积．
解答：由题意得，S△ABC=S平行四边形ABCD=12cm2，
∵E为AB的中点，
∴S△BED=S△ABD=6cm2，
又∵O是BD的中点，
∴S△OED=S△BED=3cm2．
故选A．
点评：此题考查了平行四边形的性质、三角形的面积及三角形的中位线定理，关键是掌握等高的三角形面积之比等于底边之比，难度一般，注意仔细观察图形．
分析：由图形及平行四边形的性质可得S△ABC=
S平行四边形ABCD，S△BED=S△ABD，S△OED=S△BED，从而结合平行四边形ABCD的面积为24cm2，可得出△ODE的面积．解答：由题意得，S△ABC=
S平行四边形ABCD=12cm2，∵E为AB的中点，
∴S△BED=
S△ABD=6cm2，又∵O是BD的中点，
∴S△OED=
S△BED=3cm2．故选A．
点评：此题考查了平行四边形的性质、三角形的面积及三角形的中位线定理，关键是掌握等高的三角形面积之比等于底边之比，难度一般，注意仔细观察图形．
练习册系列答案
相关题目
CD的边长a等于点P，Q间的距离．
如图，已知平行四边形ABCD的对角线AC，BD相交于点O，BD绕点O顺时针旋转交AB，DC于E，F．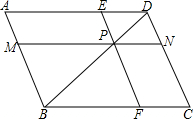
交AB、CD、AD、BC于M、N、E、F，设a=PM•PE，b=PN•PF．
23、如图，已知平行四边形ABCD．
如图，已知平行四边形ABCD，作DE⊥AB，垂足为E，把三角形AED沿AB方向平移AB长个单位长度．