题目内容
 如图,已知?ABCD的对角线AC、BD相交于点O,AC=12,BD=18,且△AOB的周长l=23,求AB的长.
如图,已知?ABCD的对角线AC、BD相交于点O,AC=12,BD=18,且△AOB的周长l=23,求AB的长.
解:∵?ABCD的对角线AC、BD相交于点O,AC=12,BD=18,
∴AO= AC=6,
AC=6,
BO= BD=9.
BD=9.
又∵△AOB的周长l=23,
∴AB=l-(AO+BO)=23-(6+9)=8.
分析:根据平行四边形中两条对角线相互平分的性质可求解.
点评:本题主要考查了平行四边形的性质及三角形的周长的计算.
∴AO=
 AC=6,
AC=6,BO=
 BD=9.
BD=9.又∵△AOB的周长l=23,
∴AB=l-(AO+BO)=23-(6+9)=8.
分析:根据平行四边形中两条对角线相互平分的性质可求解.
点评:本题主要考查了平行四边形的性质及三角形的周长的计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 14、如图,已知?ABCD中,AB=4,BC=6,BC边上的高AE=2,则DC边上的高AF的长是
14、如图,已知?ABCD中,AB=4,BC=6,BC边上的高AE=2,则DC边上的高AF的长是

 26、如图,已知?ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.
26、如图,已知?ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.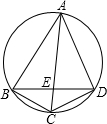 如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于
如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于 如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.
如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.