ƒøƒ⁄»ð
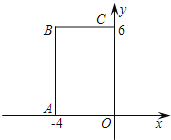
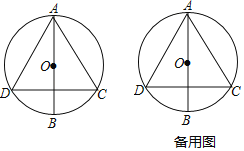
°æƒø°ø»ÁÕº1£¨![]() µƒ”ý«–÷µŒ™2£¨
µƒ”ý«–÷µŒ™2£¨![]() £¨µ„D «œþ∂Œ
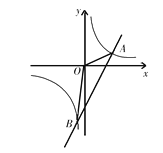
£¨µ„D «œþ∂Œ![]() …œµƒ“ª∂ص„£®µ„D≤ª”ε„A°¢B÷ÿ∫œ£©£¨“‘µ„DŒ™∂•µ„µƒ’˝∑Ω–Œ
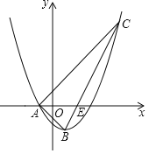
…œµƒ“ª∂ص„£®µ„D≤ª”ε„A°¢B÷ÿ∫œ£©£¨“‘µ„DŒ™∂•µ„µƒ’˝∑Ω–Œ![]() µƒ¡Ì¡Ω∏ˆ∂•µ„E°¢F∂º‘⁄…‰œþ
µƒ¡Ì¡Ω∏ˆ∂•µ„E°¢F∂º‘⁄…‰œþ![]() …œ£¨«“µ„F‘⁄µ„Eµƒ”“≤ý£¨¡™Ω·
…œ£¨«“µ„F‘⁄µ„Eµƒ”“≤ý£¨¡™Ω·![]() £¨≤¢—”≥§
£¨≤¢—”≥§![]() £¨Ωª…‰œþ
£¨Ωª…‰œþ![]() ”⁄µ„P£Æ
”⁄µ„P£Æ
£®1£©µ„D‘⁄‘À∂Ø ±£¨œ¬¡–µƒœþ∂Œ∫ÕΩ«÷–£¨________ « º÷’±£≥÷≤ª±‰µƒ¡ø£®ÃÓ–Ú∫≈£©£ª
¢Ÿ![]() £ª¢⁄
£ª¢⁄![]() £ª¢€
£ª¢€![]() £ª¢Ð
£ª¢Ð![]() £ª¢ð
£ª¢ð![]() £ª¢Þ
£ª¢Þ![]() £ª
£ª
£®2£©…Ë’˝∑Ω–Œµƒ±þ≥§Œ™x£¨œþ∂Œ![]() µƒ≥§Œ™y£¨«Ûy”Îx÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£¨≤¢–¥≥ˆ∂®“”ڣª
µƒ≥§Œ™y£¨«Ûy”Îx÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£¨≤¢–¥≥ˆ∂®“”ڣª
£®3£©»Áπ˚![]() ”Î
”Î![]() œýÀ∆£¨µ´√ʪ˝≤ªœýµ»£¨«Û¥À ±’˝∑Ω–Œµƒ±þ≥§£Æ
œýÀ∆£¨µ´√ʪ˝≤ªœýµ»£¨«Û¥À ±’˝∑Ω–Œµƒ±þ≥§£Æ
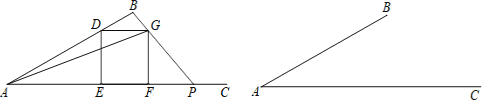
°æ¥∞∏°ø£®1£©¢Ð¢ð£ª£®2£©![]() £ª£®3£©
£ª£®3£©![]() ªÚ
ªÚ![]() .
.
°æΩ‚Œˆ°ø
£®1£©◊˜![]() ”⁄M£¨Ωª
”⁄M£¨Ωª![]() ”⁄N£¨»ÁÕº£¨¿˚”√»˝Ω«∫Ø ˝µƒ∂®“µ√µΩ
”⁄N£¨»ÁÕº£¨¿˚”√»˝Ω«∫Ø ˝µƒ∂®“µ√µΩ![]() £¨…Ë
£¨…Ë![]() £¨‘Ú
£¨‘Ú![]() £¨¿˚”√π¥π…∂®¿Ìµ√
£¨¿˚”√π¥π…∂®¿Ìµ√![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨º¥
£¨º¥![]() £¨
£¨![]() £¨…Ë’˝∑Ω–Œµƒ±þ≥§Œ™x£¨‘Ú
£¨…Ë’˝∑Ω–Œµƒ±þ≥§Œ™x£¨‘Ú![]() £¨
£¨![]() £¨”…”⁄
£¨”…”⁄![]() £¨‘Úø…≈–∂œ
£¨‘Úø…≈–∂œ![]() Œ™∂®÷µ£ª‘Ÿ¿˚”√
Œ™∂®÷µ£ª‘Ÿ¿˚”√![]() µ√µΩ
µ√µΩ![]() £¨‘Úø…≈–∂œ
£¨‘Úø…≈–∂œ![]() Œ™∂®÷µ£ª‘⁄
Œ™∂®÷µ£ª‘⁄![]() ÷–£¨¿˚”√π¥π…∂®¿Ì∫Õ»˝Ω«∫Ø ˝ø…≈–∂œ
÷–£¨¿˚”√π¥π…∂®¿Ì∫Õ»˝Ω«∫Ø ˝ø…≈–∂œ![]() ‘⁄±‰ªØ£¨
‘⁄±‰ªØ£¨![]() ‘⁄±‰ªØ£¨
‘⁄±‰ªØ£¨![]() ‘⁄±‰ªØ£ª
‘⁄±‰ªØ£ª
£®2£©“◊µ√Àƒ±þ–Œ![]() Œ™æÿ–Œ£¨‘Ú
Œ™æÿ–Œ£¨‘Ú![]() £¨÷§√˜
£¨÷§√˜![]() £¨¿˚”√œýÀ∆±»ø…µ√µΩy”Îxµƒπÿœµ Ω£ª
£¨¿˚”√œýÀ∆±»ø…µ√µΩy”Îxµƒπÿœµ Ω£ª
£®3£©”…”⁄![]() £¨
£¨![]() ”Î
”Î![]() œýÀ∆£¨«“√ʪ˝≤ªœýµ»£¨¿˚”√œýÀ∆±»µ√µΩ
œýÀ∆£¨«“√ʪ˝≤ªœýµ»£¨¿˚”√œýÀ∆±»µ√µΩ![]() £¨Ã÷¬€£∫µ±µ„P‘⁄µ„Fµ„”“≤ý ±£¨‘Ú
£¨Ã÷¬€£∫µ±µ„P‘⁄µ„Fµ„”“≤ý ±£¨‘Ú![]() £¨À˘“‘
£¨À˘“‘![]() £¨µ±µ„P‘⁄µ„Fµ„◊Û≤ý ±£¨‘Ú
£¨µ±µ„P‘⁄µ„Fµ„◊Û≤ý ±£¨‘Ú![]() £¨À˘“‘
£¨À˘“‘![]() £¨»ª∫Û∑÷±Ω‚∑Ω≥ú¥ø…µ√µΩ’˝∑Ω–Œµƒ±þ≥§£Æ
£¨»ª∫Û∑÷±Ω‚∑Ω≥ú¥ø…µ√µΩ’˝∑Ω–Œµƒ±þ≥§£Æ
£®1£©»ÁÕº£¨◊˜![]() ”⁄M£¨Ωª
”⁄M£¨Ωª![]() ”⁄N£¨
”⁄N£¨
‘⁄![]() ÷–£¨°þ
÷–£¨°þ![]() £¨
£¨
…Ë![]() £¨‘Ú
£¨‘Ú![]() £¨
£¨
°þ![]() £¨
£¨
°ý![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨
°ý![]() £¨
£¨![]() £¨
£¨
…Ë’˝∑Ω–Œµƒ±þ≥§Œ™x£¨
‘⁄![]() ÷–£¨°þ
÷–£¨°þ![]() £¨
£¨
°ý![]() £¨
£¨
°ý![]() £¨
£¨
‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨
°ý![]() Œ™∂®÷µ£ª
Œ™∂®÷µ£ª
°þ![]() £¨
£¨
°ý![]() £¨
£¨
°ý![]() Œ™∂®÷µ£ª
Œ™∂®÷µ£ª
‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨
∂¯![]() ‘⁄±‰ªØ£¨
‘⁄±‰ªØ£¨
°ý![]() ‘⁄±‰ªØ£¨
‘⁄±‰ªØ£¨![]() ‘⁄±‰ªØ£¨
‘⁄±‰ªØ£¨
°ý![]() ‘⁄±‰ªØ£¨
‘⁄±‰ªØ£¨
À˘“‘![]() ∫Õ
∫Õ![]() « º÷’±£≥÷≤ª±‰µƒ¡ø£ª
« º÷’±£≥÷≤ª±‰µƒ¡ø£ª

π ¥∞∏Œ™£∫¢Ð¢ð
£®2£©°þMN°ÕAP£¨DEFG «’˝∑Ω–Œ£¨
°ýÀƒ±þ–Œ![]() Œ™æÿ–Œ£¨
Œ™æÿ–Œ£¨
°ý![]() £¨
£¨
°þ![]() £¨
£¨
°ý![]() £¨
£¨
°ý![]() £¨
£¨
º¥![]() £¨
£¨
°ý![]()
£®3£©°þ![]() £¨
£¨![]() ”Î
”Î![]() œýÀ∆£¨«“√ʪ˝≤ªœýµ»£¨
œýÀ∆£¨«“√ʪ˝≤ªœýµ»£¨
°ý![]() £¨º¥
£¨º¥![]() £¨
£¨
°ý![]() £¨
£¨
µ±µ„P‘⁄µ„Fµ„”“≤ý ±£¨AP=AF+PF=![]() =
=![]() £¨
£¨
°ý![]() £¨
£¨
Ω‚µ√![]() £¨
£¨
µ±µ„P‘⁄µ„Fµ„◊Û≤ý ±£¨![]() £¨
£¨
°ý![]() £¨
£¨
Ω‚µ√![]() £¨
£¨

◊€…œÀ˘ ˆ£¨’˝∑Ω–Œµƒ±þ≥§Œ™![]() ªÚ
ªÚ![]() £Æ
£Æ

 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏