Question

如图，在直角坐标系中，四边形OABC为矩形，A（8，0），C（0，6），点M是OA的中点，P、Q两点同时从点M出发，点P沿x轴向右运动；点Q沿x轴先向左运动至原点O后，再向右运动到点M停止，点P随之停止运动．P、Q两点运动的速度均为每秒1个单位．以P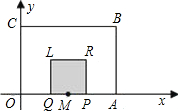Q为一边向上作正方形PRLQ．设点P的运动时间为t（秒），正方形PRLQ与矩形OABC重叠部分（阴影部分）的面积为S（平方单位）．
（1）用含t的代数式表示点P的坐标；
（2）分别求当t=1，t=5时，线段PQ的长；
（3）求S与t之间的函数关系式；
（4）连接AC．当正方形PRLQ与△ABC的重叠部分为三角形时，直接写出t的取值范围．

Answer 1

（1）∵MP=t，OM=4，
∴OP=t+4，
∴P（t+4，0）（0≤t≤8）．
（2）当t=1时，PQ=2×1=2．
当t=5时，OP=9，OQ=5-4=1，
∴PQ=9-1=8．
（3）如图①，当0≤t≤3时，
∵PQ=2t，
∴S=4t²．
如图②，当3＜t≤4时，
∵PQ=2t，AB=6，
∴S=12t．
如图③，当4＜t≤8时，
∵AQ=4-（t-4）+4=12-t，AB=6，
∴S=-6t+72．

（4）如图④，当点R在AC上时，如图6，

∵RP∥OC，
∴△APR∽△AOC，
∴

AP

OA

=

PR

OC

，
∴

4-t

8

=

2t

6

，
∴t=

12

11

．
当点L在AC上时，如图7，

同理得出

LQ

OC

=

AQ

OA

，
∴

2t

6

=

4+t

8

，
t=

12

5

，
∴

12

11

＜t≤

12

5

．
如图⑤，当点L在y轴上时，t=4．

综上可得：

12

11

＜t≤

12

5

或t=4．