题目内容
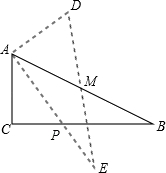
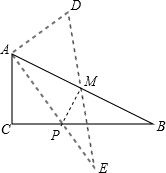
如图,在△ABC中,∠C=90°,AB=10,tanB=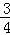 ,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
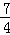 .
.
【考点】旋转的性质.
【分析】连接PM,根据∠B的正切值设AC=3k,BC=4k,利用勾股定理列式求出k值,得到AC、BC的长,根据直角三角形斜边上的中线等于斜边的一半可得AM=DM=EM,再根据等边对等角的性质可得∠EAM=∠E,然后求出∠EAM=∠B,根据等腰三角形三线合一的性质可得PM⊥AB,然后求出△ABC和△PMB相似,根据相似三角形对应边成比例列式求出PB的长,再根据CP=BC﹣PB代入数据进行计算即可得解.
【解答】解:连接PM,∵tanB= ,
,
∴设AC=3k,BC=4k,
则(3k)2+(4k)2=102,
解得k=2,
∴AC=3×2=6,BC=4×2=8,
∵点M是AB边的中点,△DEA是△ABC绕点M旋转得到,
∴AM=MB=DM=EM=5,
∴∠EAM=∠E,
又∵∠B=∠E,
∴∠EAM=∠B,
∴△APB是等腰三角形,
∵点M是AB的中点,
∴PM⊥AB,
∴△ABC∽△PMB,
∴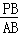 =
=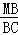 ,
,
即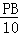 =
=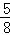 ,
,
解得P B=
B= ,
,
∴CP=BC﹣PB=8﹣ =
= .
.
故答案为: .
.
【点评】本题考查了旋转的性质,直角三角形斜边上的中线等于斜边的一半的性质,勾股定理的应用,相似三角形的判定与性质,作辅助线构造出相似三角形是解题的关键,也是本题的难点.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 (B)
(B)
 (D)
(D)


 B.
B. C.
C. D.
D. =__________.
=__________. ,
,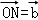 ,试在该网格中作向量
,试在该网格中作向量
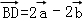 .计算:
.计算: =__________;
=__________;