题目内容
测得一弹簧的长度L(cm)与悬挂物的质量x(kg)有下面一组对应值:
试根据表中各对应值解答下列问题.
(1)用代数式表示悬挂质量为x kg的物体时的弹簧长度L;
(2)求所挂物体质量为10kg时,弹簧长度是多少?
(3)若测得弹簧长度为19cm,判断所挂物体质量是多少千克?
| 悬挂物体质量x(kg) | 0 | 1 | 2 | 3 | 4 | … |
| 弹簧长度L(cm) | 12 | 12.5 | 13 | 13.5 | 14 | … |
(1)用代数式表示悬挂质量为x kg的物体时的弹簧长度L;
(2)求所挂物体质量为10kg时,弹簧长度是多少?
(3)若测得弹簧长度为19cm,判断所挂物体质量是多少千克?
考点:函数的表示方法,函数关系式,函数值
专题:
分析:(1)观察即可得规律:弹簧称所挂重物质量x与弹簧长度L之间是一次函数关系,然后由待定系数法求解即可;
(2)将x=10代入解析式,求出L的值,即可求得答案;
(3)将L=19代入求出即可.
(2)将x=10代入解析式,求出L的值,即可求得答案;
(3)将L=19代入求出即可.
解答:解:(1)∵弹簧称所挂重物质量x(g)与弹簧长度L(cm)之间是一次函数关系,
∴设L=kx+b,
取点(0,12)与(1,12.5),
则
,
解得:
,
故L与x之间的关系式为L=0.5x+12;
(2)当x=10时,
L=0.5×10+12=17,
答:当所挂物体的质量为10千克时,弹簧的长度是17厘米.
(3)当L=19cm,则19=0.5x+12,
解得:x=14,
答:所挂物体质量是14千克.
∴设L=kx+b,
取点(0,12)与(1,12.5),
则
|
解得:
|
故L与x之间的关系式为L=0.5x+12;
(2)当x=10时,
L=0.5×10+12=17,
答:当所挂物体的质量为10千克时,弹簧的长度是17厘米.
(3)当L=19cm,则19=0.5x+12,
解得:x=14,
答:所挂物体质量是14千克.
点评:此题考查了一次函数的应用.解题的关键是根据题意求得一次函数的解析式.

练习册系列答案
相关题目
 你能将一张图形彩纸,折叠2次后沿虚线只剪1次,展开后得到一个是( )
你能将一张图形彩纸,折叠2次后沿虚线只剪1次,展开后得到一个是( )A、 |
B、 |
C、 |
D、 |
点P(3,2)关于y轴对称点的坐标是( )
| A、(3,-2) |
| B、(-3,2) |
| C、(3,2) |
| D、(-3,-2) |
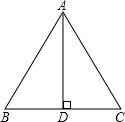 如图,已知AD是△ABC的BC边上的高,补充下列一个条件不能使△ABD≌△ACD的条件是( )
如图,已知AD是△ABC的BC边上的高,补充下列一个条件不能使△ABD≌△ACD的条件是( )| A、∠B=45° |
| B、BD=CD |
| C、AD平分∠BAC |
| D、AB=AC |
若
=
=
=2,且b+d+f=4,则a+c+e=( )
| a |
| b |
| c |
| d |
| e |
| f |
| A、2 | B、4 | C、6 | D、8 |
 如图,在平面直角坐标系中,△ABC的顶点都在网格点上.其中,A点坐标为(2,-1),则△ABC的面积为
如图,在平面直角坐标系中,△ABC的顶点都在网格点上.其中,A点坐标为(2,-1),则△ABC的面积为