题目内容
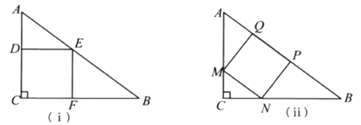
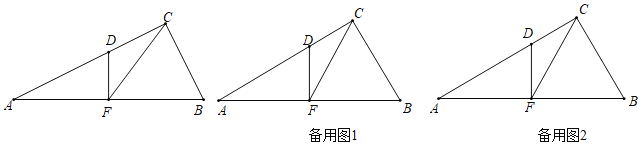
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=12,点F是AB的中点,过点F作FD⊥AB交AC于点D.
(1)若△AFD以每秒2个单位长度的速度沿射线FB向右移动,得到△A1F1D1,当F1与点B重合时停止移动.设移动时间为t秒,△A1F1D1与△CBF重叠部分的面积记为S.直接写出S与t的函数关系式.
(2)在(1)的基础上,如果D1,B,F构成的△D1BF为等腰三角形,求出t值.
【答案】(1)(1)当0<t≤1时, S=2![]() t2;当1<t≤2时, S=﹣
t2;当1<t≤2时, S=﹣![]() t2+6
t2+6![]() t﹣3
t﹣3![]() ;当2<t≤3时,﹣
;当2<t≤3时,﹣![]() t2+12
t2+12![]() t﹣9
t﹣9![]() ;(2)t的值为3﹣
;(2)t的值为3﹣![]() 或
或![]() 或
或![]() .
.
【解析】
(1)分三种情形:①如图1中,当0<t≤2时,重叠部分是△PFF1.②如图2中,当2<t≤4时,重叠部分是四边形FPD1F1.③如图3中,当4<t≤6时,重叠部分是五边形FQRPF1.分别求解即可解决问题.
(2)分三种情形:BD=D1F,BD=BD1,D1F=D1B分别求解即可.
解:(1)①如图1中,当0<t≤1时,重叠部分是△PFF1,
∵∠ACB=90°,∠A=30°,点F是AB的中点,FD⊥AB
∴∠B=60°,CF=BF
∴△FBC为等边三角形
∴∠P FF1=60°
∴∠FPF1=30°
由题意可得FF1=2t
∴PF=2 FF1=4t,根据勾股定理可得PF1=![]() 2
2![]() t
t
S=![]() FF1PF1=
FF1PF1=![]() ×2t2
×2t2![]() t=2
t=2![]() t2.
t2.
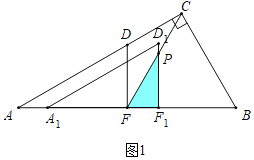
②如图2中,当1<t≤2时,重叠部分是四边形FPD1F1,过点P作PH⊥AB于

∵AF=![]() AB=6
AB=6
在△AFD中,设DF=![]() =x,则AD=2x
=x,则AD=2x
根据勾股定理可得x2+62=(2x)2
解得:x=2![]()
由题意可得FF1=2t
∴FA1=6-2t ,
∵∠FPA1=∠CFH-∠PA1F=30°
∴PF= FA1=6-2t ,
∴PH=![]() PF=
PF=![]() (3﹣t)
(3﹣t)
S=![]() ﹣
﹣![]() =
=![]() AF·DF﹣
AF·DF﹣![]() A1F·PH=﹣
A1F·PH=﹣![]() t2+6
t2+6![]() t﹣3
t﹣3![]() .
.
③如图3中,当2<t≤3时,重叠部分是五边形FQRPF1,过点Q作QH⊥AB
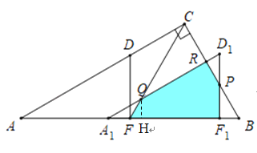
由②同理FA1=6-2t ,QH=![]() (3﹣t)
(3﹣t)
∴BF1=BF-FF1=6-2t,PF1=![]() BF1=
BF1=![]() (6-2t)
(6-2t)
∴D1P=DF-PF1=2![]() t-4
t-4![]() ,
,
∴D1R=![]() D1P=
D1P=![]() t-2
t-2![]() ,PR=
,PR=![]() D1P=3t-6
D1P=3t-6
由平移可知∠BRQ=∠BCA=90°
∴∠D1RP=90°
S=![]() ﹣
﹣![]() ﹣
﹣![]() =
=![]() AF·DF﹣
AF·DF﹣![]() A1F·PH﹣
A1F·PH﹣![]() D1R·PR=﹣
D1R·PR=﹣![]() t2+12
t2+12![]() t﹣9
t﹣9![]() .
.
综上所述:当0<t≤1时, S=2![]() t2;当1<t≤2时, S=﹣
t2;当1<t≤2时, S=﹣![]() t2+6
t2+6![]() t﹣3
t﹣3![]() ;当2<t≤3时,﹣
;当2<t≤3时,﹣![]() t2+12
t2+12![]() t﹣9
t﹣9![]() ;
;
(2)①如图4中,当BF=BD1=6时,
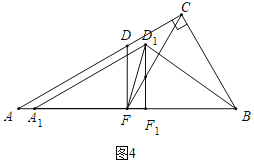
在Rt△BF1D1中,BF1=![]() =
=![]() =2
=2![]() ,
,
∴AA1=FF1=6﹣2![]() ,
,
∴t=AA1÷2=3﹣![]() .
.
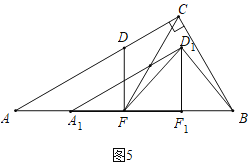
②如图5中,当D1F=D1B时,
∵D1F1⊥FB
∴AA1=FF1=F1B=3,
∴t=AA1÷2=![]() .
.
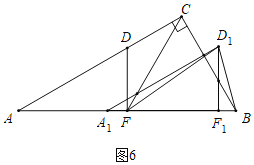
③如图6中,当FD1=FB=6时,
根据勾股定理可得FF1=![]()
∴AA1=FF1=2![]() ,
,
∴t=AA1÷2=![]() ,
,
综上所述,满足条件的t的值为3﹣![]() 或
或![]() 或
或![]() .
.