题目内容
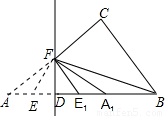 如图,直角三角形ABC中,∠ACB=90°,AB=10,BC=6,在线段AB上取一点D,作DF⊥AB交AC于点F,现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为A1;AD的中点E的对应点记为E1,若△E1FA1∽△E1BF,则AD= .
如图,直角三角形ABC中,∠ACB=90°,AB=10,BC=6,在线段AB上取一点D,作DF⊥AB交AC于点F,现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为A1;AD的中点E的对应点记为E1,若△E1FA1∽△E1BF,则AD= .
【答案】分析:利用勾股定理列式求出AC,设AD=2x,得到AE=DE=DE1=A1E1=x,然后求出BE1,再利用相似三角形对应边成比例列式求出DF,然后利用勾股定理列式求出E1F,然后根据相似三角形对应边成比例列式求解得到x的值,从而可得AD的值.
解答:解:∵∠ACB=90°,AB=10,BC=6,
∴AC=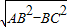 =
=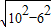 =8,
=8,
设AD=2x,
∵点E为AD的中点,将△ADF沿DF折叠,点A对应点记为A1,点E的对应点为E1,
∴AE=DE=DE1=A1E1=x,
∵DF⊥AB,∠ACB=90°,∠A=∠A,
∴△ABC∽△AFD,
∴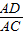 =
=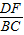 ,
,
即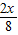 =
=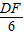 ,
,
解得DF= x,
x,
在Rt△DE1F中,E1F=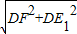 =
=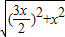 =
=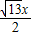 ,
,
又∵BE1=AB-AE1=10-3x,△E1FA1∽△E1BF,
∴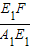 =
= ,
,
∴E1F2=A1E1•BE1,
即(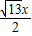 )2=x(10-3x),
)2=x(10-3x),
解得x= ,
,
∴AD的长为2× =
=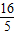 .
.
故答案为: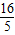 .
.
点评:本题考查了相似三角形的性质,主要利用了翻折变换的性质,勾股定理,相似三角形对应边成比例,综合题,熟记性质并准确识图是解题的关键.
解答:解:∵∠ACB=90°,AB=10,BC=6,
∴AC=
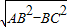 =
=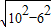 =8,
=8,设AD=2x,
∵点E为AD的中点,将△ADF沿DF折叠,点A对应点记为A1,点E的对应点为E1,
∴AE=DE=DE1=A1E1=x,
∵DF⊥AB,∠ACB=90°,∠A=∠A,
∴△ABC∽△AFD,
∴
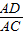 =
=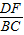 ,
,即
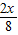 =
=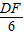 ,
,解得DF=
 x,
x,在Rt△DE1F中,E1F=
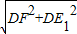 =
=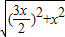 =
=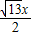 ,
,又∵BE1=AB-AE1=10-3x,△E1FA1∽△E1BF,
∴
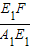 =
= ,
,∴E1F2=A1E1•BE1,
即(
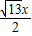 )2=x(10-3x),
)2=x(10-3x),解得x=
 ,
,∴AD的长为2×
 =
=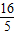 .
.故答案为:
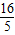 .
.点评:本题考查了相似三角形的性质,主要利用了翻折变换的性质,勾股定理,相似三角形对应边成比例,综合题,熟记性质并准确识图是解题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
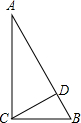 如图,直角三角形ABC中∠ACB=90°,CD是高,∠A=30°,AB=4.则BD=
如图,直角三角形ABC中∠ACB=90°,CD是高,∠A=30°,AB=4.则BD= 如图,直角三角形ABC的直角边AB=6,以AB为直径画半圆,若阴影部分的面积S1-S2=
如图,直角三角形ABC的直角边AB=6,以AB为直径画半圆,若阴影部分的面积S1-S2= 如图在直角三角形ABC的斜边AB上另作直角三角形ABD,并以AB为斜边,若BC=1,AC=m,AD=2,则BD等于( )
如图在直角三角形ABC的斜边AB上另作直角三角形ABD,并以AB为斜边,若BC=1,AC=m,AD=2,则BD等于( ) 如图,直角三角形ACB中,CD是斜边AB上的中线,若AC=8cm,BC=6cm,那么△ACD与△BCD的周长差为
如图,直角三角形ACB中,CD是斜边AB上的中线,若AC=8cm,BC=6cm,那么△ACD与△BCD的周长差为 如图,直角三角形ABC中,∠C=90°,P,E分别是边AB,BC上的点,D为△ABC外一点,DE⊥BC,DE=EC,BE=2EC,∠BDE=∠PEC,AD∥PE,AC=4,则线段BC的长为
如图,直角三角形ABC中,∠C=90°,P,E分别是边AB,BC上的点,D为△ABC外一点,DE⊥BC,DE=EC,BE=2EC,∠BDE=∠PEC,AD∥PE,AC=4,则线段BC的长为