Question

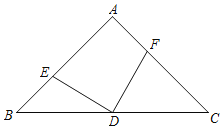
【题目】如图，在等腰直角△ABC中，∠A＝90°，AB＝AC，D为边BC中点，DE⊥DF，若四边形AEDF的面积是4，则等腰直角△ABC的面积为_____．

Answer 1

【答案】8

【解析】

先连接AD，根据等腰直角三角形的性质，求得AD＝CD，∠DAE＝∠C＝45°，∠ADE＝∠CDF，进而判定△ADE≌△CDF，得出四边形AEDF的面积＝△ACD的面积即可．

解：连接AD，

∵∠BAC＝90°，AB＝AC，D为边BC中点，

∴AD⊥BC，AD＝CD，∠DAE＝∠C＝45°，

∴∠ADE+∠ADF＝∠CDF+∠ADF＝90°，

∴∠ADE＝∠CDF，

在△ADE和△CDF中，

，

∴△ADE≌△CDF（ASA），

∴△ADE的面积＝△CDF的面积，

∴四边形AEDF的面积＝△ACD的面积＝4，

∴S△ABC＝2S△ACD＝8，

故答案为：8．