题目内容

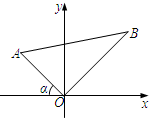如图，已知OA=2 $数学公式$ ，∠α=45°，点B的坐标为（3，3）．
求：（1）点A的坐标；
（2）直线AB的解析式；
（3）△AOB的外接圆半径．

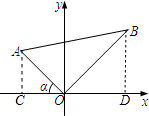解：过A、B分别作x轴的垂线，垂足分别为C、D，如图

（1）∵OA=2 $\text{[math]}$ ，∠α=45°，
∴△OAC为等腰直角三角形，
∴AC=OC= $\text{[math]}$ OA=2，
∴点A的坐标为（-2，2）；

（2）设直线AB的解析式为y=kx+b，
把A（-2，2）和点B（3，3）代入得，-2k+b=2，3k+b=3，解得k= $\text{[math]}$ ，b= $\text{[math]}$ ，
∴直线AB的解析式为y= $\text{[math]}$ x+ $\text{[math]}$ ；

（3）∵点B的坐标为（3，3），
∴△ODB为等腰直角三角形，
∴∠BOD=45°，OB= $\text{[math]}$ OD=3 $\text{[math]}$ ，
∴∠AOB=180°-45°-45°=90°，即△AOB为直角三角形，
∴AB= $\text{[math]}$ = $\text{[math]}$ ，
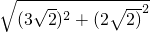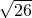∴△AOB的外接圆半径= $\text{[math]}$ = $\text{[math]}$
分析：过A、B分别作x轴的垂线，垂足分别为C、D．
（1）由OA=2 $\text{[math]}$ ，∠α=45°，可判断△OAC为等腰直角三角形，根据其性质得到AC=OC= $\text{[math]}$ OA=2，即可写出A点坐标；
（2）利用待定系数法求直线AB的解析式：设直线AB的解析式为y=kx+b，把A（-2，2）和点B（3，3）代入得，-2k+b=2，3k+b=3，解此两方程组成的方程组求出k和b即可；
（3）易得△ODB为等腰直角三角形，得到OB= $\text{[math]}$ OD=3 $\text{[math]}$ ，则有△AOB为直角三角形，然后利用勾股定理计算出AB，根据直角三角形的斜边就是其外接圆的直径可得到△AOB的外接圆半径．
点评：本题考查了利用待定系数法求直线的解析式的方法：先设直线的解析式为y=kx+b，然后把已知两点的坐标代入求出k，b即可．也考查了点的坐标与线段的关系以及等腰直角三角形的性质．