题目内容
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴,垂足为点B,反比例函数y= ![]() (x>0)的图象经过AO的中点C,且与AB相交于 点D,OB=4,AD=3
(x>0)的图象经过AO的中点C,且与AB相交于 点D,OB=4,AD=3
(1)求反比例函数y= ![]() 的解析式;
的解析式;
(2)若直线y=﹣x+m与反比例函数y= ![]() (x>0)的图象相交于两个不同点E、F(点E在点F的左边),与y轴相交于点M ①则m的取值范围为(请直接写出结果)
(x>0)的图象相交于两个不同点E、F(点E在点F的左边),与y轴相交于点M ①则m的取值范围为(请直接写出结果)
②求MEMF的值 .
【答案】
(1)解:设D的坐标是(4,a),则A的坐标是(4,a+3).
又∵点C是OA的中点,
∴点C的坐标是(2, ![]() ),
),
∴4a=2× ![]() =k,
=k,
解得a=1,k=4,
∴反比例函数的解析式为y= ![]() ;
;
(2)m>4;8
【解析】(2)①将y=﹣x+m代入y= ![]() 中,﹣x+m=
中,﹣x+m= ![]() , 整理,得:x2﹣mx+4=0,
, 整理,得:x2﹣mx+4=0,
∵直线y=﹣x+m与反比例函数y= ![]() (x>0)的图象相交于两个不同点E、F,
(x>0)的图象相交于两个不同点E、F,
∴ ![]() ,
,
解得:m>4.
所以答案是:m>4.
②解:过点E、F分别作y轴的垂线,垂足分别为G、H.
由y=﹣x+m可知:∠MEG=∠MFH=45°,
∴ME= ![]() GE,MF=
GE,MF= ![]() HF.
HF.
由y=﹣x+m= ![]() ,得x2﹣mx+4=0,
,得x2﹣mx+4=0,
∴xExF=4,
∴MEMF=2xExF=8.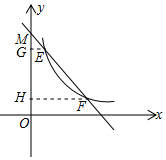

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目