题目内容
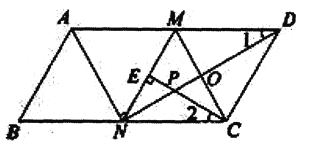
【题目】如图,有一根固定长度的木棍![]() 在正方形
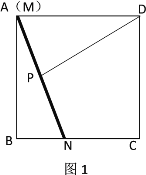
在正方形![]() 的内部如图1放置,此时木棍的端点
的内部如图1放置,此时木棍的端点![]() 恰好与点
恰好与点![]() 重合,点
重合,点![]() 在
在![]() 边上,
边上,![]() ,将木棍沿
,将木棍沿![]() 向下滑动
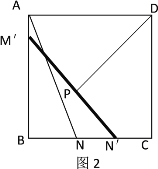
向下滑动![]() 个单位长度至图2的位置.同时另一个端点
个单位长度至图2的位置.同时另一个端点![]() 沿
沿![]() 向右滑动
向右滑动![]() 个单位长度至
个单位长度至![]() ,且
,且![]() ,
,![]() .在滑动的过程中,点
.在滑动的过程中,点![]() 到木棍中点
到木棍中点![]() 的最短距离为__________.
的最短距离为__________.
【答案】![]()
【解析】
分别根据图1和图2得出MN2=AB2+BN2=(a+3.9)2+2.52,M′N′2=BM′2+BN′2=3.92+(2.5+![]() )2,求出a值,连接BP,BD,求出BD和BP,分析出当B、P、D三点共线时,DP最短,利用DP=BD-BP得到DP的值即可.
)2,求出a值,连接BP,BD,求出BD和BP,分析出当B、P、D三点共线时,DP最短,利用DP=BD-BP得到DP的值即可.
解:由图2可知:AB=AM′+BM′=a+3.9,
∵BN=2.5,
∴在图1中,MN2=AB2+BN2=(a+3.9)2+2.52,
∵a:b=7:9,
∴![]() ,
,
在图2中,M′N′2=BM′2+BN′2=3.92+(2.5+![]() )2,
)2,
∵MN2=M′N′2,
∴(a+3.9)2+2.52=3.92+(2.5+![]() )2,
)2,
解得:a=2.1或a=0(舍),
∴AB=a+3.9=2.1+3.9=6,
∴在图1中,MN=![]() ,
,
连接BP,BD,如图,
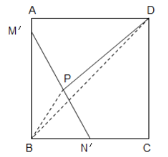
∵∠BAD=90°,AD=AB=6,
∴BD=![]() =
=![]() ,
,
∵∠M′BN′=90°,P是M′N′的中点,
∴BP=![]() M′N′=
M′N′=![]() MN=
MN=![]() ×6.5=
×6.5=![]() ,
,
∵DP≥BD-BP,
∴当B、P、D三点共线时,DP最短,此时DP=BD-BP=![]() -
-![]() ,
,
∴在滑动的过程中,点D到木棍中点P的最短距离为![]() -
-![]() .
.
故答案为:![]() -
-![]() .
.

【题目】某市居民用电的电价实行阶梯收费,收费标准如下表:
一户居民每月用电量x(单位:度) | 电费价格(单位:元/度) |
0<x≤200 | a |
200<x≤400 | b |
x>400 | 0.92 |
(1)已知李叔家四月份用电286度,缴纳电费178.76元;五月份用电316度,缴纳电费198.56元,请你根据以上数据,求出表格中a,b的值.
(2)六月份是用电高峰期,李叔计划六月份电费支出不超过300元,那么李叔家六月份最多可用电多少度?