Question

如图，在?ABCD中，∠DAB=60°，AB=15cm．已知⊙O的半径等于3cm，AB，AD分别与⊙O相切于点E，F．⊙O在?ABCD内沿AB方向滚动，与BC边相切时运动停止．试求⊙O滚过的路程？

Answer 1

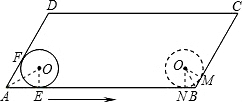解：连接OE，OA、BO．
∵AB，AD分别与⊙O相切于点E，F，
∴OE⊥AB，OE=3cm．
∵∠DAB=60°，
∴∠OAE=30°．
在Rt△AOE中，
AE=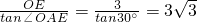cm．
∵AD∥BC，∠DAB=60°，
∴∠ABC=120°．
设当运动停止时，⊙O与BC，AB分别相切于点M，N，连接ON，OM．
同理可得，∠BON为30°，且ON为3cm，
∴BN=ON•tan30°=3×=cm，
EN=AB-AE-BN=15-3-=15-4cm．
∴⊙O滚过的路程为（15-4）cm．
分析：⊙O滚过的路程即线段EN的长度．EN=AB-AE-BN，所以只需求AE、BN的长度即可．分别解所在的直角三角形．
点评：此题考查了切线的性质、平行四边形的性质及解直角三角形等知识点，难度中等．