题目内容
 已知:如图,正方形ABCD的边长为10cm,AC是对角线,AG平分∠BAC,GH⊥AC于H.
已知:如图,正方形ABCD的边长为10cm,AC是对角线,AG平分∠BAC,GH⊥AC于H.(1)求证:BG=CH;
(2)求BG的长度.[计算中可能要用到(
| 2 |
| 2 |
分析:(1)根据角平分线性质定理可证明BG=GH,再证明三角形HGC是等腰直角三角形即可得到CH=HG,即BG=CH;
(2)由(1)可知BG=GC=HC,所以在Rt△GHC中,GC2=GH2+HC2,即
BG+BG=10cm,进而求出BG的长.
(2)由(1)可知BG=GC=HC,所以在Rt△GHC中,GC2=GH2+HC2,即
| 2 |
解答:(1)证明:∵四边形ABCD是正方形,
∴∠B=90°,
∴GB⊥AB,
∵AG平分∠BAC,GB⊥AB,GH⊥AC,
∴BG=GH,
又∵在Rt△GHC内,∠HCG=45°,
∴GH=CH,
∴BG=CH;
(2)解:∵BG+GC=10cm,且BG=GH=HC
在Rt△GHC中,GC2=GH2+HC2,
∴GC=
BG
∴
BG+BG=10cm,
即BG=
=10
-10.
∴∠B=90°,
∴GB⊥AB,
∵AG平分∠BAC,GB⊥AB,GH⊥AC,
∴BG=GH,
又∵在Rt△GHC内,∠HCG=45°,
∴GH=CH,
∴BG=CH;
(2)解:∵BG+GC=10cm,且BG=GH=HC
在Rt△GHC中,GC2=GH2+HC2,
∴GC=
| 2 |
∴
| 2 |
即BG=
| 10 | ||
|
| 2 |
点评:本题考查了正方形的性质、角平分线性质定理、等腰直角三角形的判定和性质以及勾股定理的运用,题目的综合性较强,题目的难度不大,能够很好的训练学生的解题能力.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 ,连接DF,交BE的延长线于点G,连接OG.
,连接DF,交BE的延长线于点G,连接OG.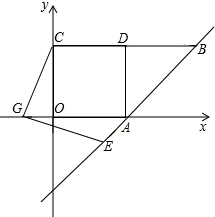
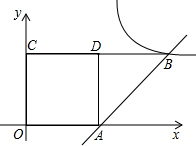
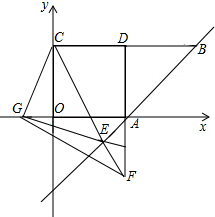



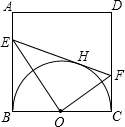 于E,交CD于F.
于E,交CD于F. 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.