题目内容
20.如果规定“Φ”为一种新的运算:aΦb=ab+a2-b2.例如:3Φ4=3×4+32-42=12+9-16=5,请仿照例题计算:
(1)-2Φ3;(2)-2Φ[(-3)Φ1].
分析 根据规定的新运算,aΦb等于两个数的乘积加上第一个的平方再减去第二个数的平方,
(1)根据新运算的含义化简(-2)Φ3,然后根据有理数混合运算的顺序,先算乘方,计算出(-2)2和32的结果,然后算乘法计算出-2×3的结果,再计算加减法即可求解;
(2)根据新运算的含义先化简中括号里面的(-3)Φ1,然后根据有理数混合运算的顺序,先算乘方,计算出(-3)2和12的结果,然后算乘法计算出-3×1的结果,再计算加减法计算出中括号里面的结果为5,然后再根据新运算的含义化简(-2)Φ5,同理也根据有理数混合运算的顺序以及法则进行正确的计算得出最后的结果.
解答 解:(1)(-2)Φ3
=-2×3+(-2)2-32
=-6+4-9
=-11;
(2)(-2)Φ[(-3)Φ1]
=(-2)Φ[(-3)×1+(-3)2-12]
=(-2)Φ(-3+9-1)
=(-2)Φ5
=(-2)×5+(-2)2-52
=-10+4-25
=-31.
点评 此题根据定义的新运算间接的考查了有理数的混合运算,解此类题的关键是搞清新运算的含义,从而根据新运算表示的含义化简要求的式子,同时也要求学生掌握有理数混合运算的运算顺序以及各种运算法则.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
10.二次根式$\sqrt{{a}^{2}}$=-a的条件是( )
| A. | a>0 | B. | a<0 | C. | a≤0 | D. | a是任意实数 |
5.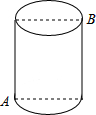 如图,一圆柱高8cm,底面半径为$\frac{6}{π}$ cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
如图,一圆柱高8cm,底面半径为$\frac{6}{π}$ cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
 如图,一圆柱高8cm,底面半径为$\frac{6}{π}$ cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
如图,一圆柱高8cm,底面半径为$\frac{6}{π}$ cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |
12.下列方程中,是一元二次方程的个数有( )
(1)$\sqrt{3}$x2+2x+1=0
(2)$\frac{1}{{x}^{2}}$+$\frac{1}{x}$+2=0
(3)x2-2x+1=0
(4)(a-1)x2+bx+c=0
(5)x2+x=4-x2.
(1)$\sqrt{3}$x2+2x+1=0
(2)$\frac{1}{{x}^{2}}$+$\frac{1}{x}$+2=0
(3)x2-2x+1=0
(4)(a-1)x2+bx+c=0
(5)x2+x=4-x2.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
9.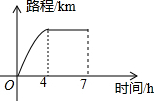 一辆汽车行驶的路程与行驶时间的关系如图所示,下列说法正确的是( )
一辆汽车行驶的路程与行驶时间的关系如图所示,下列说法正确的是( )
 一辆汽车行驶的路程与行驶时间的关系如图所示,下列说法正确的是( )
一辆汽车行驶的路程与行驶时间的关系如图所示,下列说法正确的是( )| A. | 前4h中汽车的速度越来越快 | B. | 4h后汽车静止不动 | ||
| C. | 4h后汽车以相同的速度行驶 | D. | 前4h汽车以相同速度行驶 |
 如图,是由几个相同的小正方体组成的几何体,则它的左视图是( )
如图,是由几个相同的小正方体组成的几何体,则它的左视图是( )



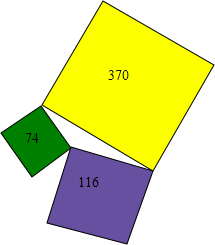 如图,一个三角形的湖被三块正方形的土地所包围,这三块正方形土地的面积分别是370英亩、116英亩和74英亩,问:这个三角形湖的面积是多少?
如图,一个三角形的湖被三块正方形的土地所包围,这三块正方形土地的面积分别是370英亩、116英亩和74英亩,问:这个三角形湖的面积是多少?