题目内容
 如图,AB=AD,AD⊥CD,BC⊥AB,AC、BD相交于E,则图中全等三角形有________对,分别为________.
如图,AB=AD,AD⊥CD,BC⊥AB,AC、BD相交于E,则图中全等三角形有________对,分别为________.
3 △ABC≌△ADC,△ABE≌△ADE,△CBE≌△CDE
分析:图中有3对全等三角形,根据HL可推出△ABC≌△ADC,推出BC=CD,∠BAE=∠DAE,∠BCE=∠DCE,根据SAS推出△ABE≌△ADE,△CBE≌△CDE即可.
解答:图中有3对全等三角形,有△ABC≌△ADC,△ABE≌△ADE,△CBE≌△CDE,
理由是:∵AD⊥CD,BC⊥AB,
∴∠ABC=∠ADC=90°,
在Rt△ABC和Rt△ADC中

∴Rt△ABC≌Rt△ADC(HL),
∴BC=CD,∠BAE=∠DAE,∠BCE=∠DCE,
在△BAE和△DAE中

∴△BAE≌△DAE(SAS),
同理可以证出△CBE≌△CDE,
故答案为:3,△ABC≌△ADC,△ABE≌△ADE,△CBE≌△CDE.
点评:本题考查了对全等三角形的判定定理的应用,注意:全等三角形的判定定理有:SAS,ASA,AAS,SSS.
分析:图中有3对全等三角形,根据HL可推出△ABC≌△ADC,推出BC=CD,∠BAE=∠DAE,∠BCE=∠DCE,根据SAS推出△ABE≌△ADE,△CBE≌△CDE即可.
解答:图中有3对全等三角形,有△ABC≌△ADC,△ABE≌△ADE,△CBE≌△CDE,
理由是:∵AD⊥CD,BC⊥AB,
∴∠ABC=∠ADC=90°,
在Rt△ABC和Rt△ADC中

∴Rt△ABC≌Rt△ADC(HL),
∴BC=CD,∠BAE=∠DAE,∠BCE=∠DCE,
在△BAE和△DAE中

∴△BAE≌△DAE(SAS),
同理可以证出△CBE≌△CDE,
故答案为:3,△ABC≌△ADC,△ABE≌△ADE,△CBE≌△CDE.
点评:本题考查了对全等三角形的判定定理的应用,注意:全等三角形的判定定理有:SAS,ASA,AAS,SSS.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
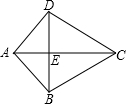 如图,AB=AD,BC=CD,AC,BD相交于E,如果不再添加辅助线,不再标注其他字母,你能找出几对全等的三角形?就其中一对三角形全等给出完整的证明过程.
如图,AB=AD,BC=CD,AC,BD相交于E,如果不再添加辅助线,不再标注其他字母,你能找出几对全等的三角形?就其中一对三角形全等给出完整的证明过程.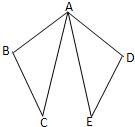 23、如图,AB=AD,∠B=∠D,∠BAC=∠DAE,AC与AE相等吗?
23、如图,AB=AD,∠B=∠D,∠BAC=∠DAE,AC与AE相等吗?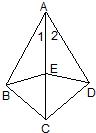 17、如图,AB=AD,BE=DE,∠1=∠2,则图中全等三角形共有
17、如图,AB=AD,BE=DE,∠1=∠2,则图中全等三角形共有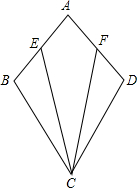 已知:如图,AB=AD,CB=CD,E、F分别是AB、AD的中点.求证:CE=CF.
已知:如图,AB=AD,CB=CD,E、F分别是AB、AD的中点.求证:CE=CF.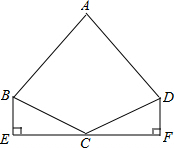 如图:AB=AD,∠ABC=∠ADC,EF过点C,BE⊥EF于E,DF⊥EF于F,BE=DF.求证:CE=CF.
如图:AB=AD,∠ABC=∠ADC,EF过点C,BE⊥EF于E,DF⊥EF于F,BE=DF.求证:CE=CF.