题目内容
设a,b都是正实数且
+
-
=0,那么
的值为( )
| 1 |
| a |
| 1 |
| b |
| 1 |
| a-b |
| b |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:把方程整理变形成含有
的方程,设
=x,建立新的关于x的方程,求得x的值后,即可得到
的值.
| b |
| a |
| b |
| a |
| b |
| a |
解答:解:由原式可得:
+
=
,
则通分化简得:
=
,
则ab=(a+b)(a-b),即ab=a2-b2,
两边同时除以a2得:
=1-
,
将
看成一个整体x,
则原关系式可变为:x=1-x2,即x2-x-1=0,
解得:x1=
,x2=
,
又因为a,b都是正实数,则
>0,
∴
=
.
故选C.
| 1 |
| a |
| 1 |
| b |
| 1 |
| a-b |
则通分化简得:
| a+b |
| ab |
| 1 |
| a-b |
则ab=(a+b)(a-b),即ab=a2-b2,
两边同时除以a2得:
| b |
| a |
| b2 |
| a2 |
将
| b |
| a |
则原关系式可变为:x=1-x2,即x2-x-1=0,
解得:x1=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
又因为a,b都是正实数,则
| b |
| a |
∴
| b |
| a |
-1+
| ||
| 2 |
故选C.
点评:解答本题需将先通分化简,再将关系式转化成一元二次方程解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,那么
,那么 的值为
的值为


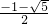
 ,那么
,那么 的值为( )
的值为( )



 ,那么
,那么 的值为( )
的值为( )


