��Ŀ����
�ı���OABC�ǵ������Σ�OA��BC���ڽ�����ͼ��ƽ��ֱ������ϵ�У�A��10��0����B��8��6����ֱ��x=4��ֱ��AC����P�㣬��x�ύ��H�㣻
��1��ֱ��д��C������꣬�����ֱ��AC�Ľ���ʽ��
��2������߶�PH�ij��ȣ�����ֱ��AC���ҵ�Q�㣬ʹ�á�PHQ�����Ϊ��AOC����� �����Q�����ꣻ
�����Q�����ꣻ
��3��M����ֱ��AC�ϳ�P�������һ�����㣬�ʣ���x�����Ƿ����N�㣬ʹ�á�MHNΪ����ֱ�������Σ����У������M�㼰��Ӧ��N������꣬��û�У���˵�����ɣ�
��1��ֱ��д��C������꣬�����ֱ��AC�Ľ���ʽ��
��2������߶�PH�ij��ȣ�����ֱ��AC���ҵ�Q�㣬ʹ�á�PHQ�����Ϊ��AOC�����
 �����Q�����ꣻ
�����Q�����ꣻ��3��M����ֱ��AC�ϳ�P�������һ�����㣬�ʣ���x�����Ƿ����N�㣬ʹ�á�MHNΪ����ֱ�������Σ����У������M�㼰��Ӧ��N������꣬��û�У���˵�����ɣ�

�⣺��1����CE��OA�ڵ�E��BF��OA��F��
���CEO=��BFA=90�㣬CE��BF��
��OA��BC��
���ı���ECBF��ƽ���ı��Σ�
��CE=BF��
���ı���OABC�ǵ������Σ�
��OC=AB��
���OEC�ա�AFB��
��OE=AF��
��A��10��0����B��8��6����
��0A=10��OF=8��BF=6��
��OE=2
��C��2��6��
��ֱ��AC����A��10��0����C��2��6����
��ֱ��AC����ʽΪ��y=kx+b��k��0��
��������ã�
��ã�k= ��b=
��b= ��
��
��ֱ��AC��y= x+
x+
��2����x=4������������ʽ��y= ����PH=
����PH=
��Q����ֱ��AC�ϣ���Q������Ϊ��t�� t+
t+ ��
��
����֪�� PH
PH |t��4|=
|t��4|= ��
�� OA
OA |yC|��
|yC|��
���t= ��
�� ��
��
�����������Q�����������ֱ���Q1�� ��
�� ����Q2��
����Q2�� ��
�� ��
��
��3���������������M���N�㣮
��M��������a�� a+
a+ ������a��10ʱ������������ĵ㣻
������a��10ʱ������������ĵ㣻
������MNH=90�㣬��MN=HN���� a+
a+ =|a��4|��
=|a��4|��
���a= ��14��
��14��
��ʱM������Ϊ�� ��
�� ����14��18����
����14��18����
������HMN=90�㣬���M��MM���x�ύ��M��㣬��H M��=M��N=M M�䣬���ϣ���M������Ϊ�� ��
�� ��ʱ��N������ΪN1��
��ʱ��N������ΪN1�� ��0����N2��
��0����N2�� ��0������M������Ϊ����14��18��ʱ��N������ΪN3����14��0����N4����32��0��
��0������M������Ϊ����14��18��ʱ��N������ΪN3����14��0����N4����32��0��

���CEO=��BFA=90�㣬CE��BF��
��OA��BC��
���ı���ECBF��ƽ���ı��Σ�
��CE=BF��
���ı���OABC�ǵ������Σ�
��OC=AB��
���OEC�ա�AFB��
��OE=AF��
��A��10��0����B��8��6����
��0A=10��OF=8��BF=6��
��OE=2
��C��2��6��
��ֱ��AC����A��10��0����C��2��6����
��ֱ��AC����ʽΪ��y=kx+b��k��0��
��������ã�

��ã�k=
 ��b=
��b= ��
����ֱ��AC��y=
 x+
x+
��2����x=4������������ʽ��y=
 ����PH=
����PH=
��Q����ֱ��AC�ϣ���Q������Ϊ��t��
 t+
t+ ��
������֪��
 PH
PH |t��4|=
|t��4|= ��
�� OA
OA |yC|��
|yC|�����t=
 ��
�� ��
�������������Q�����������ֱ���Q1��
 ��
�� ����Q2��
����Q2�� ��
�� ��
�� ��3���������������M���N�㣮
��M��������a��
 a+
a+ ������a��10ʱ������������ĵ㣻
������a��10ʱ������������ĵ㣻������MNH=90�㣬��MN=HN����
 a+
a+ =|a��4|��
=|a��4|�����a=
 ��14��
��14����ʱM������Ϊ��
 ��
�� ����14��18����
����14��18���� ������HMN=90�㣬���M��MM���x�ύ��M��㣬��H M��=M��N=M M�䣬���ϣ���M������Ϊ��
 ��
�� ��ʱ��N������ΪN1��
��ʱ��N������ΪN1�� ��0����N2��
��0����N2�� ��0������M������Ϊ����14��18��ʱ��N������ΪN3����14��0����N4����32��0��
��0������M������Ϊ����14��18��ʱ��N������ΪN3����14��0����N4����32��0��

��ϰ��ϵ�д�
 �ܿ�����ĩ��̾�ϵ�д�
�ܿ�����ĩ��̾�ϵ�д�
�����Ŀ
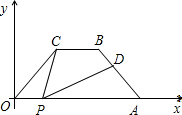 A=45�㣬��PΪx����һ�����㣬����P����O��A�غϣ�������CP������P��PD��AB�ڵ�D��
A=45�㣬��PΪx����һ�����㣬����P����O��A�غϣ�������CP������P��PD��AB�ڵ�D�� ��COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬��PD��
��COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬��PD��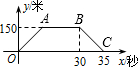 ��2012•�²���ģ�⣩������ͨ������ʱ�����������ڵij���y���ף������ʻʱ��x���룩֮��Ĺ�ϵ��ͼ��������ͼ��ʾ�������ı���OABC�ǵ������Σ������н�������ȷ���ǣ�������
��2012•�²���ģ�⣩������ͨ������ʱ�����������ڵij���y���ף������ʻʱ��x���룩֮��Ĺ�ϵ��ͼ��������ͼ��ʾ�������ı���OABC�ǵ������Σ������н�������ȷ���ǣ�������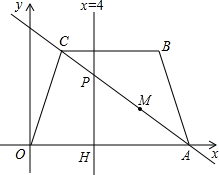 �ı���OABC�ǵ������Σ�OA��BC���ڽ�����ͼ��ƽ��ֱ������ϵ�У�A��10��0����B��8��6����ֱ��x=4��ֱ��AC����P�㣬��x�ύ��H�㣻
�ı���OABC�ǵ������Σ�OA��BC���ڽ�����ͼ��ƽ��ֱ������ϵ�У�A��10��0����B��8��6����ֱ��x=4��ֱ��AC����P�㣬��x�ύ��H�㣻 ��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��