题目内容
已知:如图,抛物线y=-
x2+3与x轴交于点A,点B,与直 线y=-
线y=-
x+b相交于点B,点C,直线y=-
x+b与y轴交于点E.
(1)求△ABC的面积;
(2)若点M在线段AB上以每秒1个单位长度的速度从A向B运动(不与A,B重合),同时,点N在射线BC上以每秒2个单位长度的速度从B向C运动,设运动时间为t秒,请写出△MNB的面积S与t的函数关系式,并求出点M运动多少时间时,△MNB的面积最大,最大面积是多少?
| 3 |
| 4 |
 线y=-
线y=-| 3 |
| 4 |
| 3 |
| 4 |
(1)求△ABC的面积;
(2)若点M在线段AB上以每秒1个单位长度的速度从A向B运动(不与A,B重合),同时,点N在射线BC上以每秒2个单位长度的速度从B向C运动,设运动时间为t秒,请写出△MNB的面积S与t的函数关系式,并求出点M运动多少时间时,△MNB的面积最大,最大面积是多少?
分析:(1)令y=0代入y=-
x2+3求出点A,B的坐标.把B点坐标代入y=-
x+b求出BC的解析式,联立方程组求出B.C的坐标.求出AB,CD的长后可求出三角形ABC的面积.
(2)过N点作NP⊥MB,证明△BNP∽△BEO,由已知令y=0求出点E的坐标,利用线段比求出NP,BE的长.求出S与t的函数关系式后利用二次函数的性质求出S的最大值.
| 3 |
| 4 |
| 3 |
| 4 |
(2)过N点作NP⊥MB,证明△BNP∽△BEO,由已知令y=0求出点E的坐标,利用线段比求出NP,BE的长.求出S与t的函数关系式后利用二次函数的性质求出S的最大值.
解答: 解:(1)在y=-
解:(1)在y=-
x2+3中,令y=0,
∴-
x2+3=0,
∴x1=2,x2=-2,
∴A(-2,0),B(2,0),
又点B在y=-
x+b上
∴0=-
+b,b=
,
∴BC的解析式为y=-
x+
.
由
,
得
,
.
∴C(-1,
),B(2,0),
∴AB=4,CD=
,
∴S△ABC=
×4×
=
.
(2)
过点N作NP⊥MB于点P
∵EO⊥MB,
∴NP∥EO,
∴△BNP∽△BEO,
∴
=
,
由直线y=-
x+
可得:E(0,
)
∴在△BEO中,BO=2,EO=
,则BE=
∴
=
,
∴NP=
t,
∴S=
×
t×(4-t)
=-
t2+
t
=-
(t-2)2+
,(0<t<4)
∵此抛物线开口向下,
∴当t=2时,S最大=
,
∴当点M运动2秒时,△MNB的面积达到最大,最大为
.
 解:(1)在y=-
解:(1)在y=-| 3 |
| 4 |
∴-
| 3 |
| 4 |
∴x1=2,x2=-2,
∴A(-2,0),B(2,0),
又点B在y=-
| 3 |
| 4 |
∴0=-
| 3 |
| 2 |
| 3 |
| 2 |
∴BC的解析式为y=-
| 3 |
| 4 |
| 3 |
| 2 |
由
|
得
|
|
∴C(-1,
| 9 |
| 4 |
∴AB=4,CD=
| 9 |
| 4 |
∴S△ABC=
| 1 |
| 2 |
| 9 |
| 4 |
| 9 |
| 2 |
(2)
过点N作NP⊥MB于点P
∵EO⊥MB,
∴NP∥EO,
∴△BNP∽△BEO,
∴
| BN |
| BE |
| NP |
| EO |
由直线y=-
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
∴在△BEO中,BO=2,EO=
| 3 |
| 2 |
| 5 |
| 2 |
∴
| 2t | ||
|
| NP | ||
|
∴NP=
| 6 |
| 5 |
∴S=
| 1 |
| 2 |
| 6 |
| 5 |
=-
| 3 |
| 5 |
| 12 |
| 5 |
=-
| 3 |
| 5 |
| 12 |
| 5 |
∵此抛物线开口向下,
∴当t=2时,S最大=
| 12 |
| 5 |
∴当点M运动2秒时,△MNB的面积达到最大,最大为
| 12 |
| 5 |
点评:此题主要考查了二次函数图象与应用相结合的综合题以及三角形面积的计算方法和相似三角形的判定与性质,利用两函数联立得出B,C坐标是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
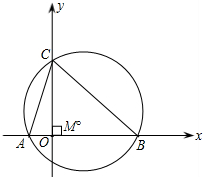 与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M.
与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, (2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(
(2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A( 已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0).
已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0). 已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.
已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.