题目内容
计算
① ×
×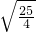
②
③| -
- |+|
|+| -1|-
-1|-
④先化简,再求值:(x-2)2-(x+3)(x-3)+(x3-4x)÷x,其中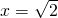
⑤已知a、b满足 ,求a2+b2的平方根.
,求a2+b2的平方根.
解:①原式=0.4×
=1;
②原式=-6+5+3
=2;
③原式= -
- +
+ -1-15
-1-15
= -16;
-16;
④原式=(x2-4x+4)-(x2-9)+(x2-4)
=x2-4x+4-x2+9+x2-4
=x2-4x+9
当x= 时,原式=2-4
时,原式=2-4 +9=11-4
+9=11-4 ;
;
⑤根据题意得: ,
,
解得: ,
,
则a2+b2=5,
因而a2+b2的平方根是:± .
.
分析:①首先把每个根式进行化简,然后相乘即可;
②首先化简每个三次根式,然后进行加减运算即可;
③首先根据绝对值的性质去掉绝对值符号,然后合并同类二次根式即可;
④首先利用完全平方公式以及平方差公式进行化简,然后合并同类项,最后代入数值计算即可求解;
⑤首先根据非负数的性质即可得到一个关于a、b的方程组,求得a、b的值,然后即可求解.
点评:本题考查的是整式的混合运算,二次根式的化简,三次根式的化简,乘法公式以及非负数的性质:几个非负数的和等于0,则每个数一定是0.

=1;
②原式=-6+5+3
=2;
③原式=
 -
- +
+ -1-15
-1-15=
 -16;
-16;④原式=(x2-4x+4)-(x2-9)+(x2-4)
=x2-4x+4-x2+9+x2-4
=x2-4x+9
当x=
 时,原式=2-4
时,原式=2-4 +9=11-4
+9=11-4 ;
;⑤根据题意得:
 ,
,解得:
 ,
,则a2+b2=5,
因而a2+b2的平方根是:±
 .
.分析:①首先把每个根式进行化简,然后相乘即可;
②首先化简每个三次根式,然后进行加减运算即可;
③首先根据绝对值的性质去掉绝对值符号,然后合并同类二次根式即可;
④首先利用完全平方公式以及平方差公式进行化简,然后合并同类项,最后代入数值计算即可求解;
⑤首先根据非负数的性质即可得到一个关于a、b的方程组,求得a、b的值,然后即可求解.
点评:本题考查的是整式的混合运算,二次根式的化简,三次根式的化简,乘法公式以及非负数的性质:几个非负数的和等于0,则每个数一定是0.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
