题目内容
【题目】某商场为了迎接“6.1儿童节“,以调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如表:
第1个 | 第2个 | 第3个 | 第4个 | … | 第n个 | |
调整前单价x (元) | x1 | x2=6 | x3=72 | x4 | … | xn |
调整后单价y (元) | y1 | y2=4 | y3=59 | y4 | … | yn |
当这些玩具调整后的单价都大于2元时,解答下列问题:
(1)y与x的函数关系式为,x的取值范围为;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了元;
(3)这n个玩具调整前、后的平均单价分别为 ![]() (元)、
(元)、 ![]() (元),猜想
(元),猜想 ![]() 与
与 ![]() 的关系式,并写出推导过程.
的关系式,并写出推导过程.
【答案】
(1)解:设y=kx+b,把(6,4),(72.59)代入得到 ![]() ,
,
解得 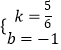
∴y= ![]() x﹣1(x>
x﹣1(x> ![]() ).
).
(2)解:当x=108时,y=89,
108﹣89=19,
∴顾客购买这个玩具省了19元.
(3)猜想: ![]() =
= ![]() ﹣1
﹣1
证明:y1= ![]() x1﹣1,y2=
x1﹣1,y2= ![]() x2﹣1,…,yn=
x2﹣1,…,yn= ![]() xn﹣1
xn﹣1
∴ ![]() =
= ![]() (y1+y2+…+yn)
(y1+y2+…+yn)
= ![]() (
( ![]() x1﹣1+
x1﹣1+ ![]() x2﹣1+…+
x2﹣1+…+ ![]() xn﹣1)
xn﹣1)
= ![]()
= ![]() =
= ![]() ﹣1.
﹣1.
【解析】(1)设y=kx+b,把(6,4),(72.59)代入得到 ![]() ,解方程组即可.(2)利用(1)的关系式求出y,求差即可解决问题.(3)猜想:
,解方程组即可.(2)利用(1)的关系式求出y,求差即可解决问题.(3)猜想: ![]() =
= ![]() ﹣1,根据平均单价的定义,列出式子计算即可.
﹣1,根据平均单价的定义,列出式子计算即可.

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
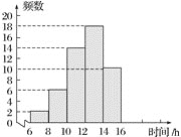
超能学典应用题题卡系列答案【题目】某地某月1~20日中午12时的气温(单位:℃)如下:
22 31 25 15 18 23 21 20 27 17
20 12 18 21 21 16 20 24 26 19
(1)将下列频数分布表补充完整:
气温分组(℃) | 划记 | 频数 |
12≤x<17 |
| 3 |
17≤x<22 | ________ | _______ |
22≤x<27 | _________ | ________ |
27≤x<32 |
| 2 |
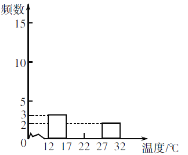
(2)补全频数分布直方图;
(3)根据频数分布表或频数分布直方图,分析数据的分布情况.