Question

如图①，矩形ABCD，AB=12cm，AD=16cm，现将其按下列步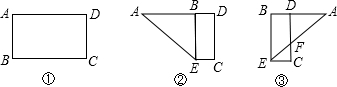骤折叠：
（1）将△BAD对折，使AB落在AD上，得到折痕AF，如图②
（2）将△AFB沿BF折叠，AF与DC交点G，如图③
则所得梯形BDGF的周长等于

1. A.
   12+2
2. B.
   24+2
3. C.
   24+4
4. D.
   12+4

Answer 1

C
分析：通过折叠，发现等腰直角三角形，表示图中相关线段的长度，再用勾股定理求FG，从而可求梯形BDGF的周长．
解答：由折叠可知，AB=BF=12，BD=CF=16-12=4，
∵△ABF为等腰直角三角形，DG∥BF，
∴△ADG为等腰直角三角形，
在图③中，DG=AD=12-4=8，
CG=CD-DG=12-8=4，
在Rt△CFG中，FG==4，
∴梯形BDGF的周长=DG+BD+BF+FG=24+4．故选C．
点评：本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后对应线段相等．