题目内容
【题目】如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则 ![]() 的值为 .
的值为 . 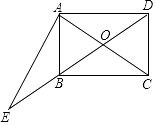
【答案】![]()
【解析】解:作BH⊥OA于H,如图,
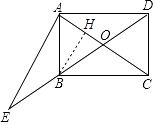
∵四边形ABCD为矩形,
∴OA=OC=OB,∠ABC=90°,
在Rt△ABC中,AC= ![]() =5,
=5,
∴AO=OB= ![]() ,
,
∵ ![]() BHAC=
BHAC= ![]() ABBC,
ABBC,
∴BH= ![]() =
= ![]() ,
,
在Rt△OBH中,OH= ![]() =
= ![]() =
= ![]() ,
,
∵EA⊥CA,
∴BH∥AE,
∴△OBH∽△OEA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() .
.
所以答案是 ![]() .
.
【考点精析】通过灵活运用矩形的性质和相似三角形的判定与性质,掌握矩形的四个角都是直角,矩形的对角线相等;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
【题目】小明利用课余时间回收废品,将卖得的钱去购买5本大小不同的两种笔记本,要求共花钱不超过28元,且购买的笔记本的总页数不低于340页,两种笔记本的价格和页数如下表.为了节约资金,小明应选择哪一种购买方案?请说明理由.
大笔记本 | 小笔记本 | |
价格(元/本) | 6 | 5 |
页数(页/本) | 100 | 60 |