Question

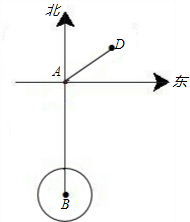
如图，一艘船以20海里/时的速度向正北航行，在A处看见灯塔C在船的北偏东30°，30min后，该船行至点B，看见灯塔C在船的北偏东60°，已知灯塔C的周围9海里以内有暗礁．
（1）求点C到直线AB的距离；
（2）若这船继续向正北航行，那么是否有触礁的危险？

Answer 1

解：（1）如图，过C作CD⊥AD于点D，
∵∠CBD=60°，∠CAB=30°，
∴∠ACB=30°，
∴BC=AB，
∵AB=20×0.5=10（海里），
∴CB=10海里，
∴=sin∠CBD=sin60°，
则CD=CB•sin60°=5，
即点C到直线AB的距离为5海里；

（2）∵5＜9，
∴继续向正北航行，有触礁的危险．
分析：（1）过C作CD⊥AD于点D，设CD长为x，根据已知分别在Rt△CBD中，在Rt△ADC中用式子表示CD，从而求得CD的长；
（2）将（1）中求得CD长度与9作比较，若大于9则没有危险，否则有危险．
点评：此题主要考查了方向角的应用，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．