题目内容
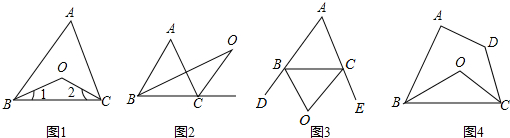
 在△ABC中,∠A是钝角,O是垂心,AO=BC,则cos(∠OBC+∠OCB)的值是
在△ABC中,∠A是钝角,O是垂心,AO=BC,则cos(∠OBC+∠OCB)的值是
- A.

- B.

- C.

- D.

A
分析:在Rt△ABD和Rt△AOF中,利用对顶角相等及互余关系可证∠1=∠2,又AO=BC,可证Rt△OAF≌Rt△BCF,可得OF=BF,△BOF为等腰直角三角形,∠BOF=45°,可知∠OBC+∠OCB=180°-45°=135°,再求cos(∠OBC+∠OCB)的值.
解答: 解:在Rt△ABD和Rt△AOF中,
解:在Rt△ABD和Rt△AOF中,
∵∠OAF=∠BAD,∠OFA=∠BDA=90°,
∴∠1=∠2,
又∵AO=BC,
∴Rt△OAF≌Rt△BCF,
∴OF=BF,△BOF为等腰直角三角形,即∠BOF=45°,
∴∠OBC+∠OCB=180°-45°=135°,
∴cos(∠OBC+∠OCB)=cos135°=- .
.
故选A.
点评:本题考查了特殊角的推导及特殊角的三角函数值的求法.关键是根据已知条件及垂心的性质证明全等三角形,特殊三角形,从而得到特殊角.
分析:在Rt△ABD和Rt△AOF中,利用对顶角相等及互余关系可证∠1=∠2,又AO=BC,可证Rt△OAF≌Rt△BCF,可得OF=BF,△BOF为等腰直角三角形,∠BOF=45°,可知∠OBC+∠OCB=180°-45°=135°,再求cos(∠OBC+∠OCB)的值.
解答:
 解:在Rt△ABD和Rt△AOF中,
解:在Rt△ABD和Rt△AOF中,∵∠OAF=∠BAD,∠OFA=∠BDA=90°,
∴∠1=∠2,
又∵AO=BC,
∴Rt△OAF≌Rt△BCF,
∴OF=BF,△BOF为等腰直角三角形,即∠BOF=45°,
∴∠OBC+∠OCB=180°-45°=135°,
∴cos(∠OBC+∠OCB)=cos135°=-
 .
.故选A.
点评:本题考查了特殊角的推导及特殊角的三角函数值的求法.关键是根据已知条件及垂心的性质证明全等三角形,特殊三角形,从而得到特殊角.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
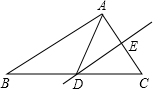 如图所示,在△ABC中,DE是AC的中垂线,AE=3cm,△ABD得周长为13cm,则△ABC的周长是
如图所示,在△ABC中,DE是AC的中垂线,AE=3cm,△ABD得周长为13cm,则△ABC的周长是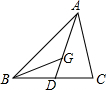 如图,在△ABC中,AD是中线,G是重心,
如图,在△ABC中,AD是中线,G是重心, 如图在△ABC中,AD是BC边上的高,BE平分∠ABD,交AD于E.已知∠BED=60°,∠BAC=50°,则∠C=( )
如图在△ABC中,AD是BC边上的高,BE平分∠ABD,交AD于E.已知∠BED=60°,∠BAC=50°,则∠C=( )