题目内容
 (2012•江干区一模)DB是⊙O的切线,D为切点,过圆上一点C作DB的垂线,垂足为B,BC=3,sin∠A=
(2012•江干区一模)DB是⊙O的切线,D为切点,过圆上一点C作DB的垂线,垂足为B,BC=3,sin∠A=| 3 |
| 4 |
分析:连接OD,CD,过C作CE垂直于OD,交OD于点E,由DB为圆O的切线,利用切线的性质得到OD垂直于DB,且弦切角等于夹弧所对的圆周角得到∠BDC=∠A,由sinA的值得出sin∠BDC的值,在直角三角形BDC中,利用锐角三角函数定义由BC的长求出CD的长,再利用勾股定理求出BD的长,由四边形BCED为矩形得到对边相等,可得出BC=ED,EC=DB,设圆的半径为r,用OD-ED表示出OE,在直角三角形OEC中,利用勾股定理列出关于r的方程,求出方程的解即可得到r的值,即为圆的半径.
解答:解:连接OD,CD,过C作CE⊥OD,交OD于点E,

∵DB为圆O的切线,
∴OD⊥DB,∠BDC=∠A,
又sinA=
,BC=3,CB⊥BD,
∴在Rt△BCD中,sin∠BDC=
=sinA=
,
解得:CD=4,
根据勾股定理得:BD=
=
,
∵四边形BCED为矩形,
∴BC=ED=3,EC=DB=
,
设OC=OD=r,则OE=OD-ED=r-3,
在Rt△OEC中,根据勾股定理得:OC2=OE2+EC2,
∴r2=(r-3)2+(
)2,
解得:r=
,
则⊙O的半径为
.
故选A

∵DB为圆O的切线,
∴OD⊥DB,∠BDC=∠A,
又sinA=
| 3 |
| 4 |
∴在Rt△BCD中,sin∠BDC=
| BC |
| CD |
| 3 |
| 4 |
解得:CD=4,
根据勾股定理得:BD=
| CD2-BC2 |
| 7 |
∵四边形BCED为矩形,
∴BC=ED=3,EC=DB=
| 7 |
设OC=OD=r,则OE=OD-ED=r-3,
在Rt△OEC中,根据勾股定理得:OC2=OE2+EC2,
∴r2=(r-3)2+(
| 7 |
解得:r=
| 8 |
| 3 |
则⊙O的半径为
| 8 |
| 3 |
故选A
点评:此题考查了切线的性质,圆周角定理,锐角三角函数定义,以及勾股定理,熟练掌握性质及定理是解本题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
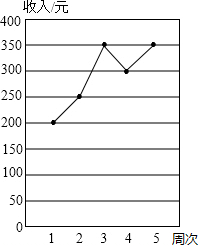 (2012•江干区一模)暑假里,小红参加了为期5周的勤工俭学活动,各周的收入情况如右图所示,以下结论中与右图反应的信息不相符的是( )
(2012•江干区一模)暑假里,小红参加了为期5周的勤工俭学活动,各周的收入情况如右图所示,以下结论中与右图反应的信息不相符的是( ) (2012•江干区一模)将矩形ABCD沿EF折叠,使点B与AD上的点B'重合,如BE=4,AB'=3,则BF的长为( )
(2012•江干区一模)将矩形ABCD沿EF折叠,使点B与AD上的点B'重合,如BE=4,AB'=3,则BF的长为( )