题目内容
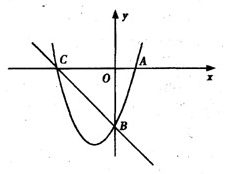
如图,已知抛物线y= x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为
x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y=
 x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
【小题1】(1)填空:点C的坐标是_ _,b=_ _;
【小题2】(2)求线段QH的长(用含t的式子表示);
【小题3】(3)依点P的变化,是否存在t的值,使以P、H、Q为顶点的三角形与△COQ相似?若存在,求出所有t的值;若不存在,说明理由.

【小题1】(1)(0,-3),b=-
 .
.【小题2】(2)由(1),得y=
 x2-
x2- x-3,它与x轴交于A,B两点,得B(4,0).
x-3,它与x轴交于A,B两点,得B(4,0).∴OB=4,又∵OC=3,∴BC=5.
由题意,得△BHP∽△BOC,
∵OC∶OB∶BC=3∶4∶5,
∴HP∶HB∶BP=3∶4∶5,
∵PB=5t,∴HB=4t,HP=3t.
∴OH=OB-HB=4-4t.
由y=
 x-3与x轴交于点Q,得Q(4t,0).
x-3与x轴交于点Q,得Q(4t,0).∴OQ=4t.
①当H在Q、B之间时,
QH=OH-OQ
=(4-4t)-4t=4-8t.··················································· 3分
②当H在O、Q之间时,
QH=OQ-OH
=4t-(4-4t)=8t-4.··················································· 4分
综合①,②得QH=|4-8t|;
【小题3】(3)存在t的值,使以P、H、Q为顶点的三角形与△COQ相似.
①当H在Q、B之间时,QH=4-8t,
若△QHP∽△COQ,则QH∶CO=HP∶OQ,得
 =
= ,
,∴t=
 .········································································· 5分
.········································································· 5分若△PHQ∽△COQ,则PH∶CO=HQ∶OQ,得
 =
= ,
,即t2+2t-1=0.
∴t1=
 -1,t2=-
-1,t2=- -1(舍去).······································· 6分
-1(舍去).······································· 6分②当H在O、Q之间时,QH=8t-4.
若△QHP∽△COQ,则QH∶CO=HP∶OQ,得
 =
= ,
,∴t=
 .········································································· 7分
.········································································· 7分若△PHQ∽△COQ,则PH∶CO=HQ∶OQ,得
 =
= ,
,即t2-2t+1=0.
∴t1=t2=1(舍去).····························································· 8分
综上所述,存在
 的值,t1=
的值,t1= -1,t2=
-1,t2= ,t3=
,t3= .解析:
.解析:略

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目