题目内容
【题目】如图,在以点O为原点的平面直角坐标系中,一次函数y=﹣ ![]() x+1的图象与x轴交于点A,与y轴交于点B,点C在直线AB上,且OC=
x+1的图象与x轴交于点A,与y轴交于点B,点C在直线AB上,且OC= ![]() AB,反比例函数y=
AB,反比例函数y= ![]() 的图象经过点C,则所有可能的k值为 .
的图象经过点C,则所有可能的k值为 . 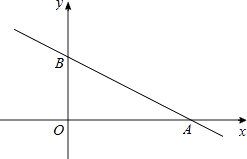
【答案】![]() 或﹣
或﹣ ![]()
【解析】解:在y=﹣ ![]() x+1中,令y=0,则x=2;令x=0,得y=1, ∴A(2,0),B(0,1).
x+1中,令y=0,则x=2;令x=0,得y=1, ∴A(2,0),B(0,1).
在Rt△AOB中,由勾股定理得:AB= ![]() .
.
设∠BAO=θ,则sinθ= ![]() ,cosθ=
,cosθ= ![]() .
.
当点C为线段AB中点时,有OC= ![]() AB,
AB,
∵A(2,0),B(0,1),
∴C(1, ![]() ).
).
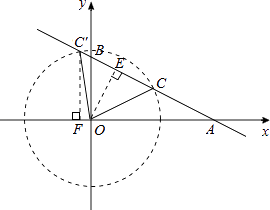
以点O为圆心,OC长为半径作圆,与直线AB的另外一个交点是C′,则点C、点C′均符合条件.
如图,过点O作OE⊥AB于点E,则AE=OAcosθ=2× ![]() =
= ![]() ,
,
∴EC=AE﹣AC= ![]() ﹣
﹣ ![]() =
= ![]() .
.
∵OC=OC′,∴EC′=EC= ![]() ,∴AC′=AE+EC′=
,∴AC′=AE+EC′= ![]() +
+ ![]() =
= ![]() .
.
过点C′作CF⊥x轴于点F,则C′F=AC′sinθ= ![]() ×
× ![]() =
= ![]() ,
,
AF=AC′cosθ= ![]() ×
× ![]() =
= ![]() ,
,
∴OF=AF﹣OA= ![]() ﹣2=
﹣2= ![]() .
.
∴C′(﹣ ![]() ,
, ![]() ).
).
∵反比例函数y= ![]() 的图象经过点C或C′,1×
的图象经过点C或C′,1× ![]() =
= ![]() ,﹣
,﹣ ![]() ×
× ![]() =﹣
=﹣ ![]() ,
,
∴k= ![]() 或﹣
或﹣ ![]() .
.
解法二:设C(m,﹣ ![]() m+1),
m+1),
根据勾股定理,m2+(﹣ ![]() m+1)2=(
m+1)2=( ![]()
![]() )2 ,
)2 ,
解得:m=﹣ ![]() 或1.
或1.
∴k= ![]() 或﹣
或﹣ ![]() .
.
所以答案是: ![]() 或﹣
或﹣ ![]() .
.

 口算题天天练系列答案
口算题天天练系列答案【题目】下表反映的是某地区电的使用量x(千瓦时)与应交电费y(元)之间的关系,下列说法不正确的是( )
用电量x(千瓦时) | 1 | 2 | 3 | 4 | … |
应交电费y(元) | 0.55 | 1.1 | 1.65 | 2.2 | … |
A. x与y都是变量,且x是自变量,y是x的函数
B. 用电量每增加1千瓦时,电费增加0.55元
C. 当交电费20.5元时,用电量为37千瓦时
D. 若用电量为8千瓦时,则应交电费4.4元