题目内容
 如图,已知点A在双曲线y=
如图,已知点A在双曲线y=| 4 |
| x |
| 17 |
分析:根据线段垂直平分线的性质可知AB=OB,故△ABC的周长=OC+AC,设OC=a,AC=b,根据勾股定理和函数解析式即可得到关于a、b的方程组,求出ab的值即可得出结论.
解答:解:∵OA的垂直平分线交OC于B,
∴AB=OB,
∴△ABC的周长=OC+AC,
设OC=a,AC=b,
则
,
解得a+b=5,即△ABC的周长=OC+AC=5.
故选B.
∴AB=OB,
∴△ABC的周长=OC+AC,
设OC=a,AC=b,
则
|
解得a+b=5,即△ABC的周长=OC+AC=5.
故选B.
点评:本题考查的是反比例函数综合题,涉及到反比例函数图象的性质和线段中垂线的性质及勾股定理的综合应用,解答此类问题的关键是一个转换思想,即把求△ABC的周长转换成求OC+AC即可解决问题.

练习册系列答案
相关题目
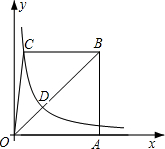 如图,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲y=
如图,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲y= 如图,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲y=
如图,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲y= 交OB于D,且OD:DB=1:2,若△OBC的面积等于4.5,则k=________.
交OB于D,且OD:DB=1:2,若△OBC的面积等于4.5,则k=________. 交OB于D,且OD:DB=1:2,若△OBC的面积等于4.5,则k= .
交OB于D,且OD:DB=1:2,若△OBC的面积等于4.5,则k= .