��Ŀ����
����Ŀ����ͼ1��������y=ax2+bx+3��x�ύ��A����3��0����B��1��0�����㣬��y�ύ�ڵ�C������AC����
��1�������������y=ax2+bx+3�Ľ���ʽ��
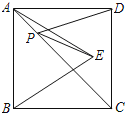
��2����ͼ2����P����Qͬʱ�ӵ�A��������P��AC��ÿ��![]() ����λ���ȵ��ٶȣ��ɵ�A���C�˶�����Q��AB��ÿ��2����λ���ȵ��ٶȣ��ɵ�A���B�˶�����һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�˶������P���˶�ʱ��Ϊt�룬����PQ��
����λ���ȵ��ٶȣ��ɵ�A���C�˶�����Q��AB��ÿ��2����λ���ȵ��ٶȣ��ɵ�A���B�˶�����һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�˶������P���˶�ʱ��Ϊt�룬����PQ��
����֤��PQ��AC��
�ڹ���Q��QE��x�ᣬ���������ڵ�E������PE����PQ=PEʱ�������t��ֵ��
����y�����Ƿ���ڵ�D��ʹ�Ե�A��P��Q��DΪ������ı�����ƽ���ı��Σ������ڣ�ֱ��д��D�����꣺�������ڣ���˵�����ɣ�

���𰸡���1��y=��x2��2x+3����2���ټ���������t��ֵΪ![]() ����D��0��1����
����D��0��1����
��������
(1)�ô���ϵ������������ʽ����2����֤����OACΪ����ֱ�������Σ���֤��APQ�ס�AOC������APQ=��AOC=90�㣬����PQ��AC������PF��x����F��PH��EQ��H�����E��2t��3��2t������E��2t��3��2t������y=��x2��2x+3�é���2t��3��2��2��2t��3��+3=3���ⷽ�̿ɵã��۽⣺���ڣ����ı���AQDPΪƽ���ı��Σ���DQ=AP=![]() t����DQO=��PAQ=45�㣬��OQ=OD=3��2t���ɵ�
t����DQO=��PAQ=45�㣬��OQ=OD=3��2t���ɵ�![]() t=
t=![]() ��3��2t�������t=1���ɵ�D������.
��3��2t�������t=1���ɵ�D������.
��1���⣺�������߽���ʽΪy=a��x+3����x��1����
��y=ax2+2ax��3a��
�ੁ3a=3�����a=��1��
�������߽���ʽΪy=��x2��2x+3��
��2����֤������x=0ʱ��y=��x2��2x+3=3����C��0��3����
���OACΪ����ֱ�������Σ�
��AC=3![]() ��
��
��AP=![]() t��AQ=2t��
t��AQ=2t��
��![]() =
=![]() t��
t��![]() =
=![]() =
=![]() t��
t��
��![]() =
=![]() ��
��
����PAQ=��OAC��
���APQ�ס�AOC��
���APQ=��AOC=90�㣬
��PQ��AC��
��֤������PF��x����F��PH��EQ��H����ͼ2����PF=AF=![]() AP=
AP=![]()
![]() t=t��
t=t��
��Q��OA�ϣ�OQ=3��2t����Q��2t��3��0����H��2t��3��t����
��Q����OB�ϣ�OQ=2t��3����Q��2t��3��0����H��2t��3��t����
��PE=PQ��
��EH=QH=t��
��E��2t��3��2t����
��E��2t��3��2t������y=��x2��2x+3�é���2t��3��2��2��2t��3��+3=3�����t1=0����ȥ����t2=![]() ��
��
��t��ֵΪ![]() ��
��
�۽⣺���ڣ�
��ͼ3�����ı���AQDPΪƽ���ı��Σ�
��DQ=AP=![]() t����DQO=��PAQ=45�㣬
t����DQO=��PAQ=45�㣬
��OQ=OD=3��2t��
��![]() t=
t=![]() ��3��2t�������t=1��
��3��2t�������t=1��
��D��0��1����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�