Question

（2012•岳阳）如图，△ABC中，AB=AC，D是AB上的一点，且AD=

2

3

AB，DF∥BC，E为BD的中点．若EF⊥AC，BC=6，则四边形DBCF的面积为

15

．

Answer 1

分析：过D点作DG⊥AC，垂足为G，过A点作AH⊥BC，垂足为H，根据题意设BE=DE=x，则AD=AF=4x，由DG∥EF，利用平行线分线段成比例求FG，由DF∥BC得△ADF∽△ABC，利用相似比求DF，同时可得∠DFG=∠C，易证Rt△DFG∽Rt△ACH，利用相似比求x，在Rt△ABH中，用勾股定理求AH，计算△ABC的面积，由△ADF∽△ABC，利用相似三角形的性质求△ADF的面积，作差求四边形DBCF的面积．

解答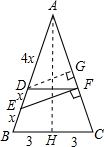：解：如图，过D点作DG⊥AC，垂足为G，过A点作AH⊥BC，垂足为H，
∵E为BD的中点，且AD=

2

3

AB，
∴可设BE=DE=x，则AD=AF=4x，
∵DG⊥AC，EF⊥AC，
∴DG∥EF，

AE

AF

=

DE

FG

，即

5x

4x

=

x

FG

，解得FG=

4

5

x，
∵DF∥BC，∴△ADF∽△ABC，

DF

BC

=

AD

AB

，即

DF

6

=

4x

6x

，
解得DF=4，
又∵DF∥BC，∴∠DFG=∠C，
∴Rt△DFG∽Rt△ACH，

DF

AC

=

FG

CH

，即

4

6x

=

4 5 x

3

，
解得x²=

5

2

，
在Rt△ABH中，由勾股定理，得AH=

AB2-BH2

=

36x2-32

=9，
则S_△ABC=

1

2

×BC×AH=

1

2

×6×9=27，
又∵△ADF∽△ABC，∴

S△ADF

S△ABC

=（

DF

BC

）²=

4

9

，
S_△ADF=

4

9

×27=12，
∴S_{四边形DBCF}=S_△ABC-S_△ADF=27-12=15，
故答案为：15．

点评：本题考查了相似三角形的判定与性质，等腰三角形的性质，勾股定理．关键是通过作辅助线，构造相似三角形，利用相似比解题．