题目内容
阅读资料:
如图1,在平面之间坐标系xOy中,A,B两点的坐标分别为A(x1,y1),B(x2,y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A,B两点间的距离为AB= .
我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系xoy中,A(x,y)为圆上任意一点,则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2,当⊙O的半径为r时,⊙O的方程可写为:x2+y2=r2.
问题拓展:如果圆心坐标为P(a,b),半径为r,那么⊙P的方程可以写为 ( 综合应用:
如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使tan∠POA=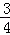 ,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
①证明AB是⊙P的切点;
②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以Q为圆心,以OQ为半径的⊙O的方程;若不存在,说明理由.
解:问题拓展:设A(x,y)为⊙P上任意一点,
∵P(a,b),半径为r,
∴AP2=(x﹣a)2+(y﹣b)2=r2.
故答案为(x﹣a)2+(y﹣b)2=r2;
综合应用:
①∵PO=PA,PD⊥OA,
∴∠OPD=∠APD.
在△POB和△PAB中,
 ,
,
∴△POB≌△PAB,
∴∠POB=∠PAB.
∵⊙P与x轴相切于原点O,
∴∠POB=90°,
∴∠PAB=90°,
∴AB是⊙P的切线;
②存在到四点O,P,A,B距离都相等的点Q.
当点Q在线段BP中点时,
∵∠POB=∠PAB=90°,
∴QO=QP=BQ=AQ.
此时点Q到四点O,P,A,B距离都相等.
∵∠POB=90°,OA⊥PB,
∴∠OBP=90°﹣∠DOB=∠POA,
∴tan∠OBP= =tan∠POA=
=tan∠POA= .
.
∵P点坐标为(0,6),
∴OP=6,OB= OP=8.
OP=8.
过点Q作QH⊥OB于H,如图3,
则有∠QHB=∠POB=90°,
∴QH∥PO,
∴△BHQ∽△BOP,
∴ =
= =
= =
= ,
,
∴QH= OP=3,BH=
OP=3,BH= OB=4,
OB=4,
∴OH=8﹣4=4,
∴点Q的坐标为(4,3),
∴OQ= =5,
=5,
∴以Q为圆心,以OQ为半径的⊙O的方程为(x﹣4)2+(y﹣3)2=25.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案2011年3月,英国和新加坡研究人员制造出观测极限为0.000 000 05米的光学显微镜,其中0.000 000 05米用科学记数法表示正确的是( )

|
| A. | 0.5×10﹣9米 | B. | 5×10﹣8米 | C. | 5×10﹣9米 | D. | 5×10﹣7米 |
 BD,连接AC,若tanB=
BD,连接AC,若tanB= ,则tan∠CAD的值( )
,则tan∠CAD的值( )




 +1)
+1) ,其中a=
,其中a= ;
; 的一元二次方程
的一元二次方程 时,配方后的方程可以是( )
时,配方后的方程可以是( ) B.
B. C.
C. D.
D.
 的解是________.
的解是________. 的图象恒有三个不同的交点,则常数m的取值范围是 .
的图象恒有三个不同的交点,则常数m的取值范围是 .