题目内容
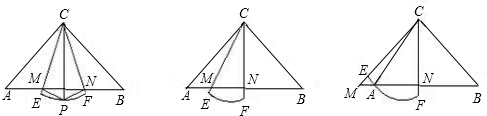
已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径长等于CA的扇形CEF绕点C旋转,直线CE、CF分别与直线AB交于点M、N.(1)如图①,当AM=BN时,将△ACM沿CM折叠,点A落在弧EF的中点P处,再将△BCN沿CN折叠,点B也恰好落在点P处,此时,PM=AM,PN=BN,△PMN的形状是
(2)如图②,当扇形CEF绕点C在∠ACB内部旋转时,线段MN、AM、BN之间的数量关系是
(3)当扇形CEF绕点C旋转至图③的位置时,线段MN、AM、BN之间的数量关系是
分析:(1)根据折叠的性质知:△CAM≌△CMP、△CNB≌△CNP,所以∠A+∠B=∠FPC+∠EPC=90°,首先可得到△PMN是直角三角形,故PM、AM、BN的数量关系符合勾股定理,即AM2+BN2=MN2;而AM=BN,所以可得到PM=PN,即△PMN是等腰直角三角形,因此PM=PN=
MN.
(2)参照(1)的思路,可将△ACM沿CM折叠,得△DCM,然后连接DN,证△DCN≌△BCN,后面的解法同(1).
(3)解法同(2).
| ||
| 2 |
(2)参照(1)的思路,可将△ACM沿CM折叠,得△DCM,然后连接DN,证△DCN≌△BCN,后面的解法同(1).
(3)解法同(2).
解答:解:(1)根据折叠的性质知:
△CAM≌△CPM,△CNB≌△CNP;
∴AM=PM,∠A=∠CPM,PN=NB,∠B=∠CPN;
∴∠MPN=∠A+∠B=90°,PM=PN=AM=BN,
故△PMN是等腰直角三角形,AM2+BN2=MN2(或AM=BN=
MN).
 (2)AM2+BN2=MN2;
(2)AM2+BN2=MN2;
将△ACM沿CM折叠,得△DCM,连DN,则△ACM≌△DCM,
∴CD=CA,DM=AM,∠DCM=∠ACM,同理可知∠DCN=∠BCN,
△DCN≌△BCN,DN=BN,而∠MDC=∠A=45°,∠CDN=∠B=45°
∴∠MDN=90°,
∴DM2+DN2=MN2,
故AM2+BN2=MN2.
(3)AM2+BN2=MN2;解法同(2).
△CAM≌△CPM,△CNB≌△CNP;
∴AM=PM,∠A=∠CPM,PN=NB,∠B=∠CPN;
∴∠MPN=∠A+∠B=90°,PM=PN=AM=BN,
故△PMN是等腰直角三角形,AM2+BN2=MN2(或AM=BN=
| ||
| 2 |
 (2)AM2+BN2=MN2;
(2)AM2+BN2=MN2;将△ACM沿CM折叠,得△DCM,连DN,则△ACM≌△DCM,
∴CD=CA,DM=AM,∠DCM=∠ACM,同理可知∠DCN=∠BCN,
△DCN≌△BCN,DN=BN,而∠MDC=∠A=45°,∠CDN=∠B=45°
∴∠MDN=90°,
∴DM2+DN2=MN2,
故AM2+BN2=MN2.
(3)AM2+BN2=MN2;解法同(2).
点评:此题主要考查了图形的翻折变换以及勾股定理的应用,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积是( )
如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积是( )A、
| ||
| B、24π | ||
C、
| ||
| D、12π |
 22、如图所示,已知Rt△ABC中,AB=AC,BD平分∠ABC,CE⊥BD交BD延长线于E,BA、CE延长线相交于F点.
22、如图所示,已知Rt△ABC中,AB=AC,BD平分∠ABC,CE⊥BD交BD延长线于E,BA、CE延长线相交于F点. 10、如图,已知Rt△ABC中,∠C=90°∠A=36°,以C为圆心,CB为半径的圆交AB于P,则弧BP的度数是
10、如图,已知Rt△ABC中,∠C=90°∠A=36°,以C为圆心,CB为半径的圆交AB于P,则弧BP的度数是 已知Rt△ABC中,∠ACB=90°,CA=CB,点D在BC的延长线上,点E在AC上,且CD=CE,延长BE交AD于点F,求证:BF⊥AD.
已知Rt△ABC中,∠ACB=90°,CA=CB,点D在BC的延长线上,点E在AC上,且CD=CE,延长BE交AD于点F,求证:BF⊥AD.