题目内容
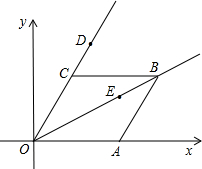 (2013•滨湖区一模)如图,菱形OABC中,点A在x轴上,顶点C的坐标为(1,
(2013•滨湖区一模)如图,菱形OABC中,点A在x轴上,顶点C的坐标为(1,| 3 |
4
4
.分析:连接AC,作B关于直线OC的对称点E′,连接AE′,交OC于D,交OB于E,此时CE+DE+BD的值最小,求出CE+DE+BD=AE′,求出∠E′BA=90°,BF=EF′=
,AB=2,根据勾股定理求出即可.
| 3 |
解答:解:连接AC,作B关于直线OC的对称点E′,连接AE′,交OC于D,交OB于E,此时CE+DE+BD的值最小,
∵四边形OCBA是菱形,
∴AC⊥OB,AO=OC,
即A和C关于OB对称,
∴CE=AE,
∴DE+CE=DE+AE=AD,
∵B和E′关于OC对称,
∴DE′=DB,
∴CE+DE+DB=AD+DE′=AE′,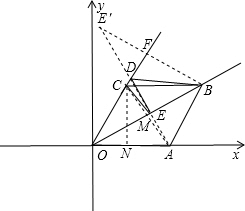
过C作CN⊥OA于N,
∵C(1,
),
∴ON=1,CN=
,
由勾股定理得:OC=2
即AB=BC=OA=OC=2,
∴∠CON=60°,
∴∠CBA=∠COA=60°,
∵四边形COAB是菱形,
∴BC∥OA,
∴∠DCB=∠COA=60°,
∵B和E′关于OC对称,
∴∠BFC=90°,
∴∠E′BC=90°-60°=30°,
∴∠E′BA=60°+30°=90°,CF=
BC=1,
由勾股定理得:BF=
=E′F,
在Rt△EBA中,由勾股定理得:AE′=
=4,
即CE+DE+DB的最小值是4.
故答案为:4.
∵四边形OCBA是菱形,
∴AC⊥OB,AO=OC,
即A和C关于OB对称,
∴CE=AE,
∴DE+CE=DE+AE=AD,
∵B和E′关于OC对称,
∴DE′=DB,
∴CE+DE+DB=AD+DE′=AE′,

过C作CN⊥OA于N,
∵C(1,
| 3 |
∴ON=1,CN=
| 3 |
由勾股定理得:OC=2
即AB=BC=OA=OC=2,
∴∠CON=60°,
∴∠CBA=∠COA=60°,
∵四边形COAB是菱形,
∴BC∥OA,
∴∠DCB=∠COA=60°,
∵B和E′关于OC对称,
∴∠BFC=90°,
∴∠E′BC=90°-60°=30°,
∴∠E′BA=60°+30°=90°,CF=
| 1 |
| 2 |
由勾股定理得:BF=
| 3 |
在Rt△EBA中,由勾股定理得:AE′=
22+(
|
即CE+DE+DB的最小值是4.
故答案为:4.
点评:本题考查了菱形性质,勾股定理,轴对称-最短路线问题的应用,关键是找出符合条件的点D和E的位置.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目


 (2013•滨湖区一模)Rt△ABC在直角坐标系内的位置如图1所示,反比例函数
(2013•滨湖区一模)Rt△ABC在直角坐标系内的位置如图1所示,反比例函数