题目内容
【题目】阅读下面材料,并回答下列问题:
小明遇到这样一个问题,如图,在![]() 中,
中,![]() 分别交
分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .已知
.已知![]() ,求
,求![]() 的值.
的值.
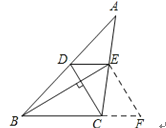
小明发现,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,构造
,构造![]() ,经过推理和计算能够使问题得到解决(如图)
,经过推理和计算能够使问题得到解决(如图)

请你回答:
(1)证明:![]() ;
;
(2)求出![]() 的值;
的值;
(3)参考小明思考问题的方法,解决问题;
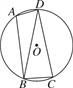
如图,已知![]() 和矩形
和矩形![]() 与
与![]() 交于点
交于点![]() .求
.求![]() 的度数.
的度数.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由DE∥BC,EF∥DC,可证得四边形DCFE是平行四边形,从而问题得以解决;
(2)由DC⊥BE,四边形DCFE是平行四边形,可得Rt△BEF,求出BF的长,证明BC+DE=BF;
(3)连接AE,CE,由四边形ABCD是平行四边形,四边形ABEF是矩形,易证得四边形DCEF是平行四边形,继而证得△ACE是等边三角形,问题得证.
(1)证明:∵DE∥BC,EF∥DC,
∴四边形DCFE是平行四边形.
∴DE=CF.
(2)解:由于四边形DCFE是平行四边形,
∴DE=CF,DC=EF,
∴BC+DE=BC+CF=BF.
∵DC⊥BE,DC∥EF,
∴∠BEF=90°.在Rt△BEF中,
∵BE=5,CD=3,
∴BF=![]() .
.
(3)连接AE,CE,如图.
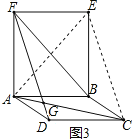
∵四边形ABCD是平行四边形,
∴AB∥DC.
∵四边形ABEF是矩形,
∴AB∥FE,BF=AE.
∴DC∥FE.
∴四边形DCEF是平行四边形.
∴CE∥DF.
∵AC=BF=DF,
∴AC=AE=CE.
∴△ACE是等边三角形.
∴∠ACE=60°.
∵CE∥DF,
∴∠AGF=∠ACE=60°.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目