题目内容
【题目】在平面上，七个边长为1的等边三角形，分别用①至⑦表示（如图）.从④⑤⑥⑦组成的图形中，取出一个三角形，使剩下的图形经过一次平移，与①②③组成的图形拼成一个正六边形.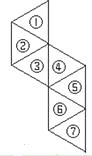
（1）你取出的是哪个三角形？写出平移的方向和平移的距离；
（2）将取出的三角形任意放置在拼成的正六边形所在平面，问：正六边形没有被三角形盖住的面积能否等于 
？请说明理由.
【答案】
（1）
解：取出的是三角形⑦；将三角形④⑤⑥组成的图形向上平移1即可得到一个正六边形.
（2）
解：可以做到.理由如下：
因为每个等边三角形的面积是 
= 
，
所以正六边形的面积 
= 
.
则0< - 
= 
< ,
所以只需要用⑦的（ ）的面积覆盖正六边形即可做到.
【解析】（1）查根据正六边形的对称性，可知要拿走⑦；（2）运用等边三角形的面积公式 
，求出一个等边三角形的面积，和正六边形的面积，只要未覆盖住的面积小于一个等边三角形的面积即可做到.
【考点精析】认真审题，首先需要了解正多边形的性质(正多边形都是轴对称图形．一个正n边形共有n条对称轴，每条对称轴都通过正n边形的中心;正多边形的中心边数为偶数的正多边形是中心对称图形，它的对称中心是正多边形的中心)．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
