Question

有一直径为

2

m的圆形纸片，要从中剪去一个最大的圆心角是90°的扇形ABC（如图）．
（1）求被剪掉的阴影部分的面积；
（2）用所留的扇形铁皮围成一个圆锥，该圆锥的底面圆的半径是多少？
（3）求圆锥的全面积．

Answer 1

（1）连接BC，∵∠A=90°，
∴BC为⊙O的直径．
在Rt△ABC中，AB=AC，且AB²+AC²=BC²，
∴AB=AC=1，
∴S_阴影=S_⊙O-S_扇形ABC=π•（

2

2

）²-

90π×12

360

=

1

2

π-

1

4

π=

1

4

π（m²）；

（2）设圆锥底面半径为r，则

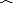BC

长为2πr．
∴

90π×1

180

=2πr，
∴r=

1

4

（m）；

（3）S_全=S_侧+S_底=S_扇形ABC+S_圆=

1

4

π+（

1

4

）²•π=

5

16

πm²．