Question

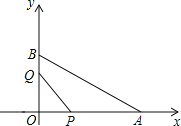
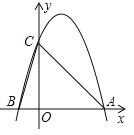
【题目】如图，△ABC、△BDE都是等腰直角三角形，BA＝BC，BD＝BE，AC＝4，DE＝．将△BDE绕点B逆时针方向旋转后得△BD'E'，当点E'恰好落在线段AD'上时，则CE'＝_______．

Answer 1

【答案】

【解析】

如图，连接CE′，过B作BH⊥CE′于H，根据等腰直角三角形的性质可得AB＝BC＝，BD＝BE＝2，根据旋转的性质可得∠D′BD＝∠ABE′，D′B＝BE′＝BD＝2，根据角的和差关系可得∠ABD′＝∠CBE′，利用SAS可证明△ABD′≌△CBE′，可得∠D′＝∠CE′B＝45°，可得出BH＝E′H＝BE′＝，利用勾股定理可求出CH的长，进而可得CE′的长.

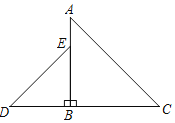
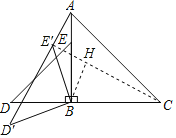
如图，连接CE′，过B作BH⊥CE′于H，

∵△ABC、△BDE都是等腰直角三角形，BA＝BC，BD＝BE，AC＝4，DE＝，

∴AB＝BC＝，BD＝BE＝2，

∵将△BDE绕点B逆时针方向旋转后得△BD′E′，

∴D′B＝BE′＝BD＝2，∠D′BE′＝90°，∠D′BD＝∠ABE′，

∴∠ABD′＝∠CBE′，

在△ABD′和△CBE中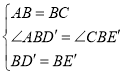

∴△ABD′≌△CBE′（SAS），

∴∠D′＝∠CE′B＝45°，

过B作BH⊥CE′于H，

在Rt△BHE′中，BH＝E′H＝BE′＝，

在Rt△BCH中，CH＝=，

∴CE′＝，

故答案为：