题目内容
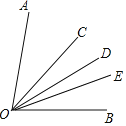
【题目】如图,已知点![]() 在同一条直线上,
在同一条直线上,![]() 平分
平分![]() .
.
(1)填空:与![]() 互余的角有 ;
互余的角有 ;
(2)若![]() ,求
,求![]() 的度数;
的度数;
(3)求证:![]() 是
是![]() 的平分线.
的平分线.

【答案】(1)![]() 、
、![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)根据互余两角的定义可得出与∠COD互余的角为∠COE,又∠COE=∠BOE,所以与∠COD互余的角还有∠BOE;
(2)根据平分线的定义,可得出∠BOE的度数,再根据平角的定义可得出结果;
(3)根据平角的定义,角平分线的定义,以及∠DOE=90°,通过角度之间的转化关系可得出结果.
解:(1)因为OE平分∠BOC,所以![]() =
=![]() ,
,
又∠DOE=90°,所以与∠DOC互余的角有![]() 、
、![]() ;
;
(2)因为![]() 平分
平分![]() ,
,
所以![]() ,
,
所以![]() ;
;
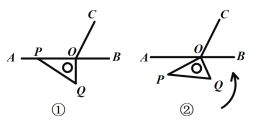
(3)证明:如图,因为![]() 是
是![]() 的平分线,
的平分线,
所以![]() .
.
因为![]() ,
,
所以![]() .
.
且![]() .
.
所以![]() .
.
所以![]() .
.
所以![]() 是
是![]() 的平分线.
的平分线.


练习册系列答案
相关题目
【题目】某校初三(1)班50名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计表如下:
自选项目 | 人数 | 频率 |
立定跳远 | 9 | 0.18 |
三级蛙跳 | 12 | a |
一分钟跳绳 | 8 | 0.16 |
投掷实心球 | b | 0.32 |
推铅球 | 5 | 0.10 |
合计 | 50 | 1 |
(1)求a,b的值;
(2)若将各自选项目的人数所占比例绘制成扇形统计图,求“一分钟跳绳”对应扇形的圆心角的度数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中至多有一名女生的概率.