题目内容
 如图,AC=2,延长正方形ABCD的一边AB到点E,使BE=BC,则DE=________.
如图,AC=2,延长正方形ABCD的一边AB到点E,使BE=BC,则DE=________.

分析:先根据勾股定理求出正方形的边长,由BE=BC可知AE=2AB,再根据勾股定理求出DE的长即可.
解答:∵四边形ABCD是正方形,AC=2,
∴AC2=
 =4,
=4,∴AB=BC=
 ,
,∵BE=BC,
∴AB=BC=BE=
 ,
,∴DE=
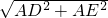 =
= =
= .
.故答案为:
 .
.点评:本题考查的是勾股定理及正方形的性质,解答此题时要注意把所求线段的长转化为求直角三角形的边长,再利用勾股定理求解.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
 26、已知:如图,?ABCD中,延长AB到E,延长CD到F,使BE=DF.
26、已知:如图,?ABCD中,延长AB到E,延长CD到F,使BE=DF. 并延长交BC的延长线于点E.过D作⊙O的切线交BC于点F.
并延长交BC的延长线于点E.过D作⊙O的切线交BC于点F.
 如图,AC=2,延长正方形ABCD的一边AB到点E,使BE=BC,则DE=
如图,AC=2,延长正方形ABCD的一边AB到点E,使BE=BC,则DE=